Question

【题目】抛物线与轴交于两点，与轴交于，其中，点为抛物线上一动点，过点作平行交抛物线于，

（1）求抛物线的解析式；

（2）①当两点重合时时，所在直线解析式为_____________．

②在①的条件下，取线段中点，连接，判断以点为顶点的四边形是什么四边形，并说明理由？

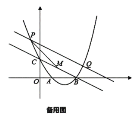
（3）已知，连接，轴，交于，轴上有一动点，，的长为______．

Answer 1

【答案】（1）；（2）①，②菱形，见解析；（3）或

【解析】

（1）将代入即可解答；

（2）①待定系数法求出直线BC的解析式，当两点重合时，即直线与抛物线只有一个交点，结合直线PQ∥BC，即可设直线PQ为，联立抛物线解析式，根据根的判别式即可求出m的值，进而得到直线PQ的解析式；

②画出图形，根据M是BC的中点，计算出BM=，联立方程组求出点P的坐标，得到OP=，从而证明四边形POMB是平行四边形，再根据OP=OM，从而证明平行四边形POMB是菱形即可；

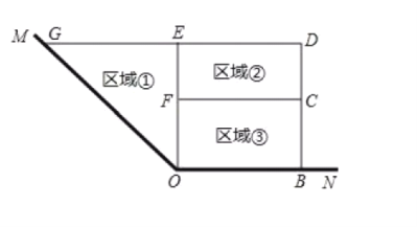
（3）求出直线BN的解析式，得出点E的坐标以及∠ONB=60°，∠OBN=30°，如图所示，以NE为边，∠ONB为内角，构造等边△HNE，并作△HNE的外接圆圆P，交x轴于点F1，F2，连接NP，EP，NF1，EF1，NF2，EF2，根据同圆中等弦所对的圆周角相等，即可确定∠NF1E=∠NF2E=∠NHE=60°，从而确定点F，根据∠PNE=∠PEN=30°，∠PEN=∠OBN=30°，得到PE∥OB，结合PN=PE，列出方程，求出点P的坐标，再由垂径定理即可求出，从而得出OF1及OF2即可．

解：（1）将代入得：

，解得：，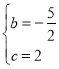

∴；

（2）①设直线BC的解析式为y=kx+a，将代入得：

，解得：，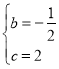

∴直线BC为：，

当两点重合时，即直线与抛物线只有一个交点，

∵直线PQ∥BC，

∴设直线PQ的解析式为，

由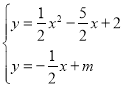，得，

∴，解得m=0，

∴直线PQ的解析式为，

故答案为：；

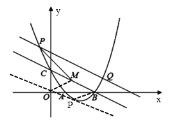
②如图，∵，点M是BC的中点，

∴M（2,1）

∴BM=，OM=，

由得，

∴P（2，-1），

∴OP=，

∵直线PQ经过原点，

∴OP∥BM，

又∵OP=BM，

∴四边形POMB是平行四边形，

又∵OP=OM=，

∴平行四边形POMB是菱形；

（3）设直线BN的解析式为y=px+q，

将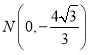，代入得：

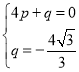，解得：，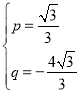

∴直线BN的解析式为：，

当x=3时，y=,

∴E，

∵OB=4，ON=，

∴tan∠ONB=，

∴∠ONB=60°，则∠OBN=30°，

如图所示，以NE为边，∠ONB为内角，构造等边△HNE，并作△HNE的外接圆圆P，交x轴于点F1，F2，连接NP，EP，NF1，EF1，NF2，EF2，

∴∠NF1E=∠NF2E=∠NHE=60°，

∵点P是△HNE的外接圆圆心，

∴NP，PE分别平分∠ONE，∠HEN，

∴∠PNE=∠PEN=30°，

∴∠PEN=∠OBN=30°，

∴PE∥OB，

∴点P的纵坐标为，

设点P为，

∵PN=PE，

∴，解得：n=1，

∴P，

∴圆P的半径为PE=2，

过点P作PG⊥x轴于点G，连接PF1，

则GP=，OG=1，PF1=2，

由垂径定理得：，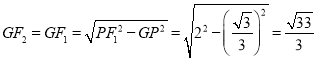

∴OF1=GF1-OG==，OF2=GF2+OG==，

故答案为：或．