Question

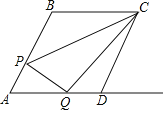
【题目】如图，矩形ABCD的对角线相交于O，E是OD的中点，DF∥AC交CE延长线于点F，连接AF．

（1）求证：四边形AODF是菱形．

（2）若∠AFC=90°，AB=2，求AD的长．

Answer 1

【答案】（1）见解析；（2）2

【解析】

(1)由“AAS”可证△DEF≌△OEC，可得DF=OC=OA，可证四边形AODF是平行四边形，且OA=OD，可得结论；
(2)由直角三角形的性质可求∠CAF=60°，可得∠OAD=30°，可证得∠OAD=∠ODA =30°，利用含30度角的直角三角形的性质即可求解．

(1)∵DF∥AC，

∴∠DFC=∠OCF，∠EDF=∠EOC，

∵DE=OE，

∴△DEF≌△OEC，

∴DF=OC ，

∵ABCD是矩形，

∴OA=OC=OD，

∴DF=OA，且DF∥AO，

∴四边形AODF是平行四边形，

∵OA =OD，

∴四边形AODF是菱形；

(2)∵四边形AODF是菱形，

∴AF=AO，

∴AC=2AF，

∵∠AFC=90°，

∴∠CAF=60°，

∴∠OAD=30°，

∵四边形ABCD是矩形，

∴∠BAD=90°，OA =OD，

∴∠OAD=∠ODA=30°，

∵AB=2，

∴AD=AB=．