题目内容
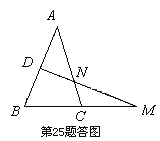
【题目】在△ABC中,AB=AC,AB的垂直平分线交AC于点N,交BC的延长线于点M,∠A=40°.
(1)求∠NMB的大小.
(2)如果将(1)中的∠A的度数改为70°,其余条件不变,再求∠NMB的大小.
(3)你认为存在什么样的规律?试用一句话说明.(请同学们自己画图)
(4)将(1)中的∠A改为钝角,对这个问题规律的认识是否需要加以修改?
【答案】(1)∠NMB=20°;(2)∠NMB=35°;(3)AB的垂直平分线与底边BC的延长线所夹的锐角等于∠A的一半;(4)见解析.
【解析】试题分析:(1)利用等腰三角形,
试题解析:
解:画出图形如图所示.
(1)∵AB=AC,
∴∠B=∠ACB,
∴∠B=![]() (180°-∠A)=70°,
(180°-∠A)=70°,
∴∠NMB=90°-∠B=90°-70°=20°.
(2)∵AB=AC,
∴∠B=∠ACB,
∴∠B=![]() (180°-∠A)=55°,
(180°-∠A)=55°,
∴∠NMB=90°-∠B=90°-55°=35°.
(3)规律:∠NMB的度数等于顶角∠A度数的一半,
证明:∵AB=AC,
∴∠B=∠ACB,
∴∠B=![]() (180°-∠A),
(180°-∠A),
∵∠BNM=90°,∴∠NMB=90°-∠B=90°-![]() (180°-∠A)=
(180°-∠A)=![]() ∠A,
∠A,
即∠NMB的度数等于顶角∠A度数的一半.
(4)将(1)中的∠A改为钝角,这个规律不需要修改,仍有等腰三角形一腰的垂直平分线与底边或底边的延长线相交所成的锐角等于顶角的一半.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目