题目内容
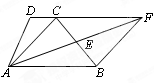
如图, 梯形ABCD中,AD∥BC,对角线的交点为O,CE∥AB交BD的延长线于E,若OB=6,OD=4,则DE=( )
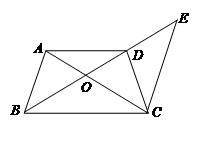
| A.12 | B.9 | C.8 | D.5 |
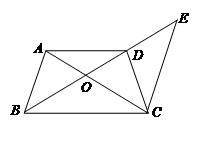
D
在梯形ABCD中,由分析可知BO:OE=AO:OC=OD:OB,
即:OD:OB=BO:OE,
又OB=6,OD=4,即4:6=6:OE,
解得OE=9,又OD=4,所以DE=5,故选D.
即:OD:OB=BO:OE,
又OB=6,OD=4,即4:6=6:OE,
解得OE=9,又OD=4,所以DE=5,故选D.

练习册系列答案
相关题目

 对角线
对角线 、
、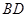 相交于点
相交于点 ,若
,若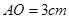 ,
, ,则菱形
,则菱形 .
.
 ,
, .
.
 垂直于线段
垂直于线段 .设图(1)、图(2)和图(3)中的四边形
.设图(1)、图(2)和图(3)中的四边形 的
的 ,
, 和
和 ,则
,则 不与点
不与点 ,
, ,
, ,
, 重合)的任意情形,请你就四边形
重合)的任意情形,请你就四边形