题目内容
(本题6分)
如图，梯形ABCD中， DC∥AB，点E是BC的中点，连结AE并延长与DC的延长线相交于点F，连结BF，AC.
求证：四边形ABFC是平行四边形；
如图，梯形ABCD中， DC∥AB，点E是BC的中点，连结AE并延长与DC的延长线相交于点F，连结BF，AC.
求证：四边形ABFC是平行四边形；
解：四边形ABFC是平行四边形．理由如下：
∵BE=CE，AB∥DC
∴△FEC≌△AEB（AAS）
∴AE=EF
∵AB∥CF
∴四边形ABFC是平行四边形．
∵BE=CE，AB∥DC
∴△FEC≌△AEB（AAS）
∴AE=EF
∵AB∥CF
∴四边形ABFC是平行四边形．
此题考查三角形全等和平行四边形的判定。
练习册系列答案
相关题目
和
. 现给出下列命题：
，则
；②若
，则DF＝2AD.
的方向运动，且点P与点B，A都不重合．图2是此运动过程中，△ABP的面积
与点P经过的路程
之间的函数图象的一部分．
时，
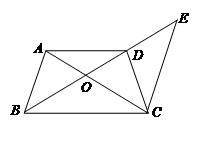
，∠C＝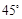
，AD＝1，BC＝4，点E为AB中点，EF∥DC交BC于点F，求EF的长。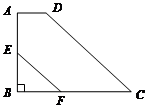
沿
折叠后，点
分别落在点
的位置，若
，则
．
如不能成功，请说明理由