题目内容
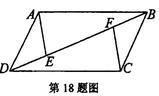
如图,梯形ABCD中, DC∥AB,点E是BC的中点,连结AE并延长与DC的延长线相交于点F,连结BF,AC.
求证:四边形ABFC是平行四边形;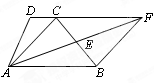
求证:四边形ABFC是平行四边形;

证明略
利用全等三角形根据平行四边形的判定来证明
证明法一:∵DC∥AB
∴∠ECF=∠EBA
∵E是BC中点
∴CE=BE
又∵∠CEF=∠BEA
∴△CEF≌△BEA(ASA)
∴CF=AB
∵CF∥AB
∴四边形ABFC是平行四边形
证明法二:同上可得,△CEF≌△BEA(ASA)
∴EF=AE
又∵CE=BE
∴四边形ABFC是平行四边形
证明法一:∵DC∥AB
∴∠ECF=∠EBA
∵E是BC中点
∴CE=BE
又∵∠CEF=∠BEA
∴△CEF≌△BEA(ASA)
∴CF=AB
∵CF∥AB
∴四边形ABFC是平行四边形
证明法二:同上可得,△CEF≌△BEA(ASA)
∴EF=AE
又∵CE=BE
∴四边形ABFC是平行四边形

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
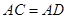 ,
,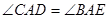 ,
,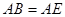
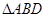 ≌
≌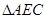 ;
;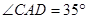 ,
,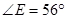 ,
,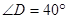 ,
,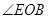 的度数
的度数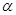 度(
度(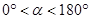 ),问当
),问当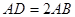 ,连接CD,若
,连接CD,若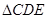 的面积为6cm2,你能求出四边形ABDC的面积吗?若能,请求出来;若不能,请你说明理由。
的面积为6cm2,你能求出四边形ABDC的面积吗?若能,请求出来;若不能,请你说明理由。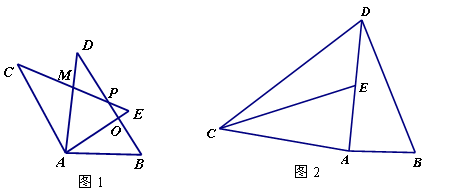
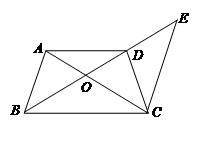
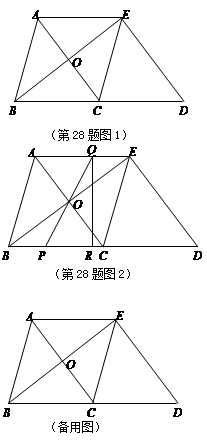
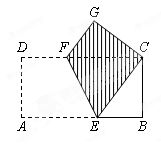
 ,沿图中线段DE、CF将△ABC剪开,分成的三块图形恰能拼成正方形CFHG,如图1所示.请你解决如下问题:
,沿图中线段DE、CF将△ABC剪开,分成的三块图形恰能拼成正方形CFHG,如图1所示.请你解决如下问题: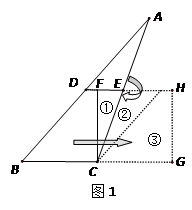
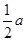 .请你设计两种不同的分割方法,将△A′B′C′沿分割线剪开后,所得的三块图形恰能拼成一个正方形,请在图2、图3中,画出分割线及拼接后的图形.
.请你设计两种不同的分割方法,将△A′B′C′沿分割线剪开后,所得的三块图形恰能拼成一个正方形,请在图2、图3中,画出分割线及拼接后的图形.
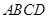 为平行四边形,
为平行四边形,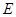 、
、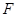 为对角线
为对角线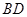 上的两点,且
上的两点,且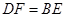 ,连接
,连接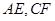 。求证:
。求证: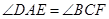 。
。