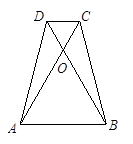题目内容
顺次连接对角线互相垂直的四边形的各边中点，所得图形一定是 （ ）
| A．矩形 | B．直角梯形 | C．菱形 | D．正方形 |
A
根据四边形对角线互相垂直，运用三角形中位线平行于第三边证明四个角都是直角，判断是矩形．
解：如图：∵E、F、G、H分别为各边中点
∴EF∥GH∥DB，EF=GH=
DB
EH=FG=AC，EH∥FG∥AC
∵DB⊥AC
∴EF⊥EH
∴四边形EFGH是矩形．
故选A．
本题考查的是三角形中位线定理的性质，比较简单，也可以利用三角形的相似，得出正确结论．
解：如图：∵E、F、G、H分别为各边中点
∴EF∥GH∥DB，EF=GH=
DBEH=FG=
AC，EH∥FG∥AC∵DB⊥AC
∴EF⊥EH
∴四边形EFGH是矩形．
故选A．
本题考查的是三角形中位线定理的性质，比较简单，也可以利用三角形的相似，得出正确结论．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
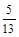，BC=26．
沿
折叠后，点
分别落在点
的位置，若
，则
．
中，
，对角线
平分
，则梯形
