��Ŀ����
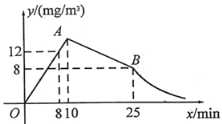
����Ŀ�����������и߷��ļ��ڣ�Ϊ�ˣ�ijУΪԤ�����У��Խ��ҽ���Ѭҩ����.�ڶԽ��ҽ��������Ĺ����У��Ⱦ���10min��ҩ��ȼ�գ��ٷ�ս���15min��Ȼ����Ŵ�����ͨ��.��֪���ڿ����к�ҩ��![]() ��ҩ���ڿ����еij���ʱ��
��ҩ���ڿ����еij���ʱ��![]() ֮��ĺ�����ϵʽ��ͼ��ʾ����ͼ���߶�OA���߶�AB��˫�����ڵ�B�����Ҳಿ�֣��������ͼ����Ϣ����������⣺
֮��ĺ�����ϵʽ��ͼ��ʾ����ͼ���߶�OA���߶�AB��˫�����ڵ�B�����Ҳಿ�֣��������ͼ����Ϣ����������⣺
��1����ҩ��ȼ�սκʹ��Ŵ�����ͨ���![]() ��
��![]() ֮��ĺ�������ʽ��
֮��ĺ�������ʽ��
��2�������ڿ����еĺ�ҩ��������![]() �ҳ���ʱ�䲻����35min��������Ч��������˴������Ƿ���Ч����˵������.
�ҳ���ʱ�䲻����35min��������Ч��������˴������Ƿ���Ч����˵������.
���𰸡���1��ҩ��ȼ�ս�y1=![]() x�����Ŵ�����ͨ���
x�����Ŵ�����ͨ���![]() ��
��
��2����Ч�����ɼ�����
��������
��1���������֪OA����ҩ��ȼ�սΣ������㣨8,12�������ɽ�����⣻���Ŵ�����ͨ���Ϊ������������������B��25,8�����ʿ���⣻��2�����AO���뷴���������κ�ҩ��Ϊ![]() ��ʱ�䣬���������ʱ�䣬���ɽ����ж�.
��ʱ�䣬���������ʱ�䣬���ɽ����ж�.
��1����ҩ��ȼ�ս�OA����ʽ��y1=k1x,�߾����㣨8,12��
��k1=![]() ����y1=
����y1=![]() x
x
����Ŵ�����ͨ���Ϊ![]() ��������B��25,8������k2=200��
��������B��25,8������k2=200��
��![]() ��
��
��2����y1=5,��x=![]() ,
,
��y2=5,��x=40,
�����ڿ����еĺ�ҩ��������![]() �ij���ʱ��Ϊ40-
�ij���ʱ��Ϊ40-![]() =
=![]() ��35���ʴ˴�������Ч.
��35���ʴ˴�������Ч.

����Ŀ��ijУ���꼶��������ѧ�������������������������������鲿��ѧ���ijɼ������ݳ�������Ƴ����µ�ͳ��ͼ��
��� | ����x | Ƶ�� |
A | 40��x��50 | 20 |
B | 50��x��60 | 30 |
C | 60��x��70 | 50 |
D | 70��x��80 | m |
E | 80��x��90 | 40 |
����������Ϣ����������⣺
��1���������������ѧ����ͳ��ͼ���У�m���������벹ȫֱ��ͼ��
��2��������ͳ��ͼ����B��������Ӧ��Բ�ĽǵĶ�����
��3�������꼶����800��ѧ��������������60��Ϊ�ϸ�������㱾�α���ȫ�꼶��
��ѧ��������