题目内容
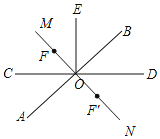
【题目】已知:如图,直线AB、CD相交于点O,EO⊥CD于O.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,请你过点O画直线MN⊥AB,并在直线MN上取一点F(点F与O不重合),然后直接写出∠EOF的度数.

【答案】(1)54°;(2)120°;(3)∠EOF的度数为30°或150°.
【解析】
(1)依据垂线的定义以及对顶角相等,即可得∠BOE的度数;
(2)依据平角的定义以及垂线的定义,即可得到∠AOE的度数;
(3)分两种情况:若F在射线OM上,则∠EOF=∠BOD=30°;若F'在射线ON上,则∠EOF'=∠DOE+∠BON-∠BOD=150°.
解:(1)∵EO⊥CD,
∴∠DOE=90°,
又∵∠BOD=∠AOC=36°,
∴∠BOE=90°-36°=54°;
(2)∵∠BOD:∠BOC=1:5,
∴∠BOD=![]() ∠COD=30°,
∠COD=30°,
∴∠AOC=30°,
又∵EO⊥CD,
∴∠COE=90°,
∴∠AOE=90°+30°=120°;
(3)分两种情况:
若F在射线OM上,则∠EOF=∠BOD=30°;
若F'在射线ON上,则∠EOF'=∠DOE+∠BON-∠BOD=150°;
综上所述,∠EOF的度数为30°或150°.
故答案为:(1)54°;(2)120°;(3)∠EOF的度数为30°或150°.

练习册系列答案
相关题目