题目内容
【题目】如图,射线AB∥CD,P为一动点,∠BAP与∠DCP的平分线AE与CE交于点E.
(1)当P在线段AC上运动时(如图1),即∠APC=180,则∠AEC=______;
(2)当P运动到图2的位置时,猜想∠AEC与∠APC 的关系,并说明理由;
(3)当P运动到图3的位置时,(2)中的结论还成立吗?(不要求说明理由)

【答案】(1)90°;(2)∠AEC=![]() ∠APC;(3)∠AEC=180°-
∠APC;(3)∠AEC=180°-![]() ∠APC..
∠APC..
【解析】
(1)根据∠BAP与∠DCP的平分线AE与CE交于点E,即可得出∠BAE=∠EAC,∠DCE=∠ACE,再利用平行线的性质求出即可;
(2)作EM∥BA,PN∥BA,根据平行的传递性,再根据两直线平行内错角相等的性质可求;
(3)根据平行的传递性,再根据两直线平行内错角相等的性质以及平角性质即可求出.
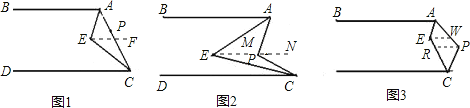 解:(1)过E作EF∥AB,
解:(1)过E作EF∥AB,
∵AB∥CD,
∴∠BAC+∠DCA=180°,
∵∠BAP与∠DCP的平分线AE与CE交于点E,
∴∠BAE=∠EAC,∠DCE=∠ACE,
∴∠BAE+∠CEF=90°;
∴∠AEC=180°,此时∠AEC为90度;
(2)作EM∥BA,PN∥BA,
∴∠BAE=∠AEM,∠MEC=∠ECD,
∠APN=∠BAP,∠NPC=∠PCD,
∵∠BAE=∠EAP,∠PCE=∠ECD,
又∵∠AEC=∠AEM+∠MEC,∠APC=∠APN+∠NPC,
∴∠AEC=![]() ∠APC;
∠APC;
(3)作EW∥AB,EP∥AB,
同理即可得出:2∠AEC=360°-∠APC,
∴∠AEC=180°-![]() ∠APC.
∠APC.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目