Question

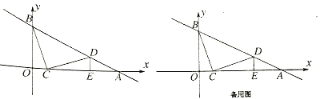
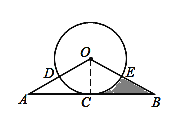
【题目】如图，AB与⊙O相切于点C，OA，OB分别交⊙O于点D,E，弧CD=弧CE．

（1）求证：OA=OB

（2）已知AB=4，OA=4，求阴影部分的面积．

Answer 1

【答案】（1）见解析；（2）

【解析】分析：（1）首先连接OC，可得OC⊥AB，然后根据圆心角、弧、弦、弦心距的关系，由弧CD=弧CE，可得∠AOC=∠BOC，进而得出∠A=∠B，利用等角对等边即可证明出结论；

（2）根据（1）可得BC的长，从而得出OC的长，然后根据三角形和扇形的面积计算可得出△BOC和扇形OCE的面积，再两部分作差即可求出阴影部分的面积.

详解：(1) 连接OC,

与⊙O相切于点C，

∠ACO=90°，

∴弧CD=弧CE

∠AOC=∠BOC，

∠A=∠B，

OA=OB，

(2 )由(1)可以知道: OAB是等腰三角形，

，

sin∠COB=,

∠COB=60°，

∠B=30°，

,

扇形OCE的面积为:，

OCB的面积为:，

S阴影=.