题目内容
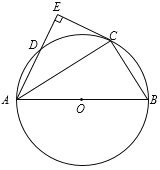
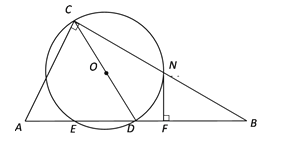
【题目】如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,与AC、BC分别交于点M、N,与AB的另一个交点为E.过点N作NF⊥AB,垂足为F.
(1)求证:NF是⊙O的切线;
(2)若NF=2,DF=1,求弦ED的长.
【答案】(1)证明见解析;(2)3.
【解析】
(1)连接ON,根据切线的判定进行证明;
(2)利用四边形ONFH为矩形的判定和垂径定理,勾股定理求解.
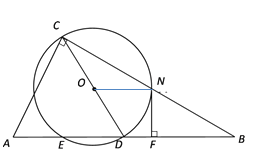
(1)证明:连接ON.
∵在Rt△ACB中,CD是边AB的中线,
∴CD=BD,
∴∠DCB=∠B,
∵OC=ON,
∴∠ONC=∠DCB,
∴∠ONC=∠B,
∴ON// AB
∵ NF⊥AB
∴∠NFB=90°
∴∠ONF=∠NFB=90°,
∴ON⊥NF
又∵NF过半径ON的外端
∴NF是⊙O的切线
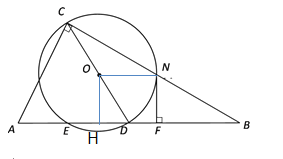
(2)过点O作OH⊥ED,垂足为H,设⊙O的半径为r
∵OH⊥ED, NF⊥AB , ON⊥NF,
∴∠OHD=∠NFH=∠ONF=90°.
∴四边形ONFH为矩形.
∴HF= ON=r,OH=NF=2
∴HD=HF-DF=r-1
在Rt△OHD中,∠OHD=90°
∴OH2+HD2=OD2
即22+(r-1)2=r2
∴r=![]() .
.
∴HD=![]()
∵OH⊥ED,且OH过圆心O
∴ED=2HD=3

【题目】某厂生产A,B两种产品,其单价随市场变化而做相应调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图: A,B产品单价变化统计表
第一次 | 第二次 | 第三次 | |
A产品单价 (元/件) | 6 | 5.2 | 6.5 |
B产品单价 (元/件) | 3.5 | 4 | 3 |

并求得了A产品三次单价的平均数和方差:![]() ;
;![]()
(1)补全图中B产品单价变化的折线图,B产品第三次的单价比上一次的单价降低了 %;
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0)使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值。
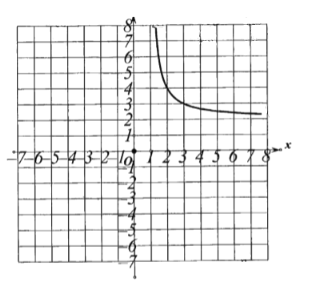
【题目】二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
| … | 5 | 0 | -3 | -4 | -3 | m | … |
(1)m= ;
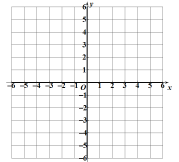
(2)在图中画出这个二次函数的图象;
(3)当![]() 时,x的取值范围是 ;
时,x的取值范围是 ;
(4)当![]() 时,y的取值范围是 .
时,y的取值范围是 .