题目内容
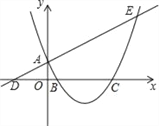
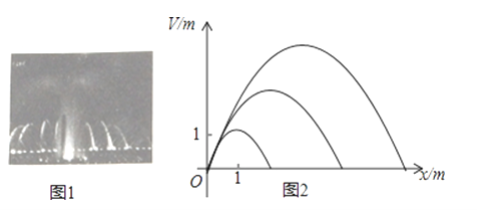
【题目】音乐喷泉(图1)可以使喷水造型随音乐的节奏起伏变化而变化.某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边18m,音乐变化时,抛物线的顶点在直线y=kx上变动,从而产生一组不同的抛物线(图2),这组抛物线的统一形式为y=ax2+bx.
(1)若已知k=1,且喷出的抛物线水线最大高度达3m,求此时a、b的值;
(2)若k=1,喷出的水恰好达到岸边,则此时喷出的抛物线水线最大高度是多少米?
(3)若k=3,a=﹣![]() ,则喷出的抛物线水线能否达到岸边?
,则喷出的抛物线水线能否达到岸边?
【答案】(1)a、b的值分别是![]() ,2;(2)喷出的抛物线水线最大高度是9米;(3)喷出的抛物线水线能达到岸边.
,2;(2)喷出的抛物线水线最大高度是9米;(3)喷出的抛物线水线能达到岸边.
【解析】
(1)根据抛物线的顶点在直线y=kx上,抛物线为y=ax2+bx,k=1,且喷出的抛物线水线最大高度达3m,可以求得a,b的值;
(2)根据k=1,喷出的水恰好达到岸边,抛物线的顶点在直线y=kx上,可以求得抛物线的对称轴x的值,从而可以得到此时喷出的抛物线水线最大高度;
(3)根据k=3,a=-![]() ,抛物线的顶点在直线y=kx上,抛物线为y=ax2+bx,可以求得b的值,然后令y=0代入抛物线的解析式,求得x的值,然后与18作比较即可解答本题.
,抛物线的顶点在直线y=kx上,抛物线为y=ax2+bx,可以求得b的值,然后令y=0代入抛物线的解析式,求得x的值,然后与18作比较即可解答本题.
(1)∵y=ax2+bx的顶点为(﹣![]() ),抛物线的顶点在直线y=kx上,k=1,抛物线水线最大高度达3m,
),抛物线的顶点在直线y=kx上,k=1,抛物线水线最大高度达3m,
∴![]() ,
,![]() ,
,
解得,a=![]() ,b=2,
,b=2,
即k=1,且喷出的抛物线水线最大高度达3m,此时a、b的值分别是![]() ,2;
,2;
(2)∵k=1,喷出的水恰好达到岸边,出水口离岸边18m,抛物线的顶点在直线y=kx上,
∴此时抛物线的对称轴为x=9,y=x=9,
即此时喷出的抛物线水线最大高度是9米;
(3)∵y=ax2+bx的顶点为(﹣![]() )在直线y=3x上,a=﹣
)在直线y=3x上,a=﹣![]() ,
,
∴![]() ,
,
解得,b=6,
∴抛物线y=![]() ,
,
当y=0时,0=![]() ,
,
解得,x1=21,x2=0,
∵21>18,
∴若k=3,a=﹣![]() ,则喷出的抛物线水线能达到岸边,
,则喷出的抛物线水线能达到岸边,
即若k=3,a=﹣![]() ,喷出的抛物线水线能达到岸边.
,喷出的抛物线水线能达到岸边.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案