题目内容
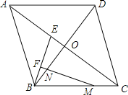
【题目】在菱形![]() 中,对角线
中,对角线![]() ,
,![]() 交于点
交于点![]() ,
,![]() 为
为![]() 上点,且
上点,且![]() ,
,![]() 为
为![]() 上点,
上点,![]() 为
为![]() 上点,且
上点,且![]() ,并与
,并与![]() 相交于点
相交于点![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的长.(结果用
的长.(结果用![]() 表示)
表示)
【答案】![]() 证明见解析;(2)
证明见解析;(2)![]()
【解析】
(1)由菱形性质得AC⊥BD,由已知得出∠CEB=∠CBE,由MF⊥BE,得出∠BOE=∠BFM,即可得出结论;
(2)作MP∥AC于BE交于点P,与OB交于点Q,由△BOE∽△MFB,得出∠EBO=∠FMB,证出tan∠OCB=![]() ,由平行线的性质得出∠MPB=∠CEB=∠CBE,∠MQN=90°,
,由平行线的性质得出∠MPB=∠CEB=∠CBE,∠MQN=90°,![]() ,证出△MBP为等腰三角形,由等腰三角形的三线合一性质得出BF=FP,∠PMF=∠BMF=∠PBQ,证得△PBQ∽△NMQ,由对应边成比例得出比例式即可求出结果.
,证出△MBP为等腰三角形,由等腰三角形的三线合一性质得出BF=FP,∠PMF=∠BMF=∠PBQ,证得△PBQ∽△NMQ,由对应边成比例得出比例式即可求出结果.
![]() ) ∵
) ∵![]() 、
、![]() 是菱形
是菱形![]() 的对角线,
的对角线,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
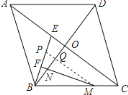
![]() 作
作![]() 与
与![]() 交于点
交于点![]() ,与
,与![]() 交于点
交于点![]() ,如图所示:
,如图所示:
由![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() 为等腰三角形,
为等腰三角形,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()

练习册系列答案
相关题目