题目内容
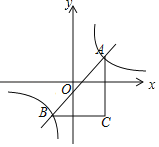
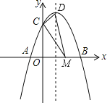
【题目】如图,对称轴为![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() 点坐标为
点坐标为![]() 设抛物线的顶点为
设抛物线的顶点为![]() .
.
![]() 求抛物线的解析式及顶点坐标;
求抛物线的解析式及顶点坐标;
![]() 为
为![]() 轴上的一点,当
轴上的一点,当![]() 的周长最小时,求点
的周长最小时,求点![]() 的坐标及
的坐标及![]() 的周长.
的周长.
【答案】(1)![]() ,顶点
,顶点![]() ;(2)
;(2)![]() ,
,![]() 的周长最小值
的周长最小值![]() .
.
【解析】
(1)根据题意得出方程组,求出b和c的值,得出抛物线的解析式,即可求出顶点坐标;
(2)求出C(0,3),得出C点关于x轴的对称点C′(0,﹣3),连接C′D交x轴于M,则△MCD的周长最小,由待定系数法求出直线C′D的解析式,即可得出M(![]() ,0),过D作DE⊥y轴于E,得出DE=1,CD=1,C′E=7,由勾股定理求出CD=
,0),过D作DE⊥y轴于E,得出DE=1,CD=1,C′E=7,由勾股定理求出CD=![]() ,C′D=5
,C′D=5![]() ,即可得出△MCD的周长最小值.
,即可得出△MCD的周长最小值.
(1)根据题意得: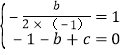 ,解得:b=2,c=3,∴抛物线的解析式为y═﹣x2+2x+3,当x=1时,y=﹣1+2+3=4,∴顶点D(1,4);
,解得:b=2,c=3,∴抛物线的解析式为y═﹣x2+2x+3,当x=1时,y=﹣1+2+3=4,∴顶点D(1,4);
(2)当x=0时,y=3,∴C(0,3),∴C点关于x轴的对称点C′(0,﹣3),连接C′D交x轴于M,则△MCD的周长最小,CM=C′M,设直线C′D的解析式为y=kx+b(k≠0),∴![]() ,∴k=7,∴y=7x﹣3,当y=0时,7x﹣3=0,解得:x=
,∴k=7,∴y=7x﹣3,当y=0时,7x﹣3=0,解得:x=![]() ,∴M(
,∴M(![]() ,0),过D作DE⊥y轴于E.
,0),过D作DE⊥y轴于E.
∵C(0,3),D(1,4),∴DE=1,CD=1,C′E=7,∴CD=![]() ,C′D=5
,C′D=5![]() ,∴△MCD的周长最小值=
,∴△MCD的周长最小值=![]() +5
+5![]() =6
=6![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目