题目内容
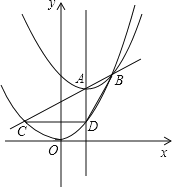
【题目】A是直线x=1上一个动点,以A为顶点的抛物线y1=a(x﹣1)2+t和抛物线y2=ax2交于点B(A,B不重合,a是常数),直线AB和抛物线y2=ax2交于点B,C,直线x=1和抛物线y2=ax2交于点D.(如图仅供参考)
(1)求点B的坐标(用含有a,t的式子表示);
(2)若a<0,且点A向上移动时,点B也向上移动,求![]() 的范围;
的范围;
(3)当B,C重合时,求![]() 的值;
的值;
(4)当a>0,且△BCD的面积恰好为3a时,求![]() 的值.
的值.
【答案】(1) 点B坐标为(![]() ,
,![]() );(2)
);(2)![]() >﹣1 ;(3)
>﹣1 ;(3) ![]() =﹣3;(4)
=﹣3;(4) ![]() 的值为﹣5或3
的值为﹣5或3
【解析】
(1)把两抛物解析式联立方程组,求得的解(含a、t的式子)即为点B坐标.
(2)由于A向上移动时,点B也向上移动,即点B纵坐标的值随点A纵坐标的值变大而变大,所以yB=![]() 随着t的增大而增大,把yB看作关于t的二次函数,可知当a<0时开口向下,故在对称轴左侧即t<a,yB随着t的增大而增大,利用不等式性质即求得
随着t的增大而增大,把yB看作关于t的二次函数,可知当a<0时开口向下,故在对称轴左侧即t<a,yB随着t的增大而增大,利用不等式性质即求得![]() ≥1且
≥1且![]() ≠1.
≠1.
(3)以点A、B坐标用待定系数法求直线AB解析式,在把直线AB和抛物线y2联立方程组另一交点C的坐标.
(4)把x=1代入y2=ax2求得点D坐标,发现点C、D纵坐标相等,即CD∥x轴,CD=2,所以△BCD面积等于CD与点B到CD距离乘积的一半.又点B到CD距离即点B与点C纵坐标之差,需分类讨论再结合a<0计算.
解:(1)∵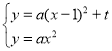 解得:
解得: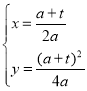
∴点B坐标为(![]() ,
,![]() )
)
(2)∵点A(1,t)向上移动,点B(![]() ,
,![]() )也向上移动
)也向上移动
∴yB=![]() 随着t的增大而增大
随着t的增大而增大
∵yB=![]() 可看作是yB关于t的二次函数
可看作是yB关于t的二次函数
∴当a<0时,此二次函数的图象开口向下,在t=﹣a时取得最大值为0
∴t<﹣a,yB随着t的增大而增大
∴![]() >﹣1
>﹣1
(3)设直线AB解析式为y=kx+b∴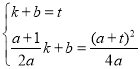 解得:
解得: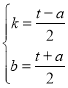
∴直线AB:y=![]() x+
x+![]()
∵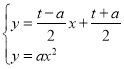 解得:
解得: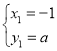
![]()
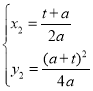 (即点B)
(即点B)
∴直线AB和抛物线y2=ax2另一交点C(﹣1,a)
∵B,C重合
∴![]()
∴a+t=﹣2a
∴3a=﹣t
∴![]() =﹣3
=﹣3
(4)∵直线x=1和抛物线y2=ax2交于点D
∴D(1,a)
∴CD∥x轴,CD=2
∴S△BCD=![]() CD|yB﹣yC|=|
CD|yB﹣yC|=|![]() ﹣a|=3a
﹣a|=3a
①当![]() ﹣a>0时,
﹣a>0时,![]() ﹣a=3a
﹣a=3a
整理得:15a2﹣2at﹣t2=0
∴(5a+t)(3a﹣t)=0
∴t=﹣5a或t=3a
∴![]() =﹣5或
=﹣5或![]() =3
=3
②当![]() ﹣a<0时,﹣
﹣a<0时,﹣![]() +a=3a
+a=3a
整理得:﹣(a+t)2=8a2
∵a>0
∴此式子不成立
综上所述,![]() 的值为﹣5或3.
的值为﹣5或3.