题目内容
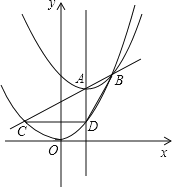
【题目】如图,一次函数y=kx+3的图象与反比例函数![]() 的图象交于P、Q两点,PA⊥x轴于点A,一次函数的图象分别交x轴、y轴于点C、点B,其中OA=6,且
的图象交于P、Q两点,PA⊥x轴于点A,一次函数的图象分别交x轴、y轴于点C、点B,其中OA=6,且![]() .
.
(1)求一次函数和反比例函数的表达式;
(2)求△APQ的面积;
(3)根据图象写出当x取何值时,一次函数的值小于反比例函数的值.

【答案】(1)y=-![]() x+3,y=-
x+3,y=-![]() ;(2)S△APQ=30;(3)当-4<x<0或x>6时,一次函数的值小于反比例函数的值.
;(2)S△APQ=30;(3)当-4<x<0或x>6时,一次函数的值小于反比例函数的值.
【解析】
(1)根据题意求得C(2,0).将C代入y=kx+3中,即可得到一次函数的表达式.
根据题意求得P(6,-6).将点P(6,-6)代入反比例函数y=![]() ,即可得到反比例函数的表达式.
,即可得到反比例函数的表达式.
(2)联立直线PQ与反比例函数解析式,得到Q点坐标.再根据三角形的面积公式即可得到答案.
(3)通过观察图像即可得到答案.
(1)∵OA=6,且![]() ,
,
∴OA=3OC=6,
∴OC=2,即C(2,0).
将C(2,0)代入y=kx+3中,
得:0=2k+3,解得:k=-![]() ,
,
∴一次函数的表达式为y=-![]() x+3.
x+3.
令y=-![]() x+3中x=6,则y=-6,
x+3中x=6,则y=-6,
∴P(6,-6).
∵点P(6,-6)在反比例函数y=![]() 的图象上,
的图象上,
∴m=6×(-6)=-36,
∴反比例函数的表达式为y=-![]() .
.
(2)联立直线PQ与反比例函数解析式,
得: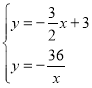 ,解得:
,解得:![]() ,或
,或![]() ,
,
∴Q(-4,9).
∴S△APQ=![]() AC(yQ-yP)=
AC(yQ-yP)=![]() ×(6-2)×[9-(-6)]=30.
×(6-2)×[9-(-6)]=30.
(3)观察函数图象发现:
当-4<x<0或x>6时,一次函数图象在反比例函数图象的下方,
∴当-4<x<0或x>6时,一次函数的值小于反比例函数的值.

【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?