题目内容
【题目】如图，在△ABC中，AB=BC，BE⊥AC于点E，AD⊥BC于点D，∠BAD=45°，CD=
，AD与BE交于点F，连接CF，则AD的长为_____．
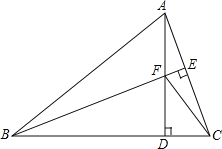
【答案】2+
【解析】
根据等腰三角形三线合一的性质得BE是AC的垂直平分线，可得AF=FC，再证明△ACD≌△BFD可得DF=DC=
，进而可得结果．
解：∵AD⊥BC，
∴∠ADB=90°，
∵∠BAD=45°，
∴∠DBA=45°，
∴AD=BD，
∵AB=BC，
BE⊥AC，
∴AE=EC
∴BE是AC的垂直平分线，
∴AF=CF，
∵∠CAD+∠ACD=90°
∠FBD+∠ACD=90°
∴∠CAD=∠FBD
∴△ACD≌△BFD(ASA)
∴DF=CD=
∴FC=
=2
∴AD=AF+FD=2+．
故答案为2+．
练习册系列答案
相关题目
