��Ŀ����
����Ŀ����ͼ��һ���ִ������͵���˫������б���ţ����Ų��ö���˫����б����ƣ������ʡ�H���Σ������ø�˿��б���̶���
���������
��β�����������������ľ���AD��
������ƣ�
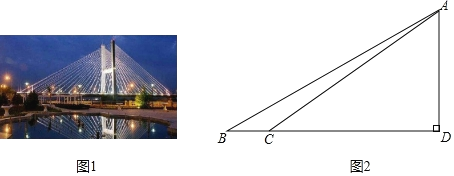
��ͼ��ij��ѧ�����о�С��ͨ�������о���ʵ�ز�����������B����á�ABC=26.57�㣬����BD������21����C������C����á�ACD=30.96�㣮
��������
�����������������ݣ�����̲�ƺӴ�����������������ľ���AD��
(�����ȷ��1m���ο����ݣ�sin26.57���0.447��cos26.57���0.894��tan26.57���0.500��sin30.96���0.514��cos30.96���0.858��tan30.96���0.600)
���𰸡���̲�ƺӴ�����������������ľ���ADΪ63�ף�
��������
�ȸ�������ó���ABD����ACD�Ķ�����BC�ij���������������Ǻ����Ķ��壬��Rt��ABD����AD��ʾBD����Rt��ACD����AD��ʾCD�������BD-CD=BC�г�AD�ķ��̣����AD��ɣ�
�⣺��������ã�
��ABD=26.57�㣬��ACD=30.96�㣬BC=21�ף�
��Rt��ABD�У���ABD=26.57�㣬
��tan��ABD![]() ��
��
��BD![]() ��
��
��Rt��ACD�У���ACD=30.96�㣬
��tan��ACD![]() ��
��
��CD![]() ��
��
��BD��CD=BC��BC=21��
��2AD![]() ��
��
��AD=63(��)��
����̲�ƺӴ�����������������ľ���ADΪ63�ף�

 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�����Ŀ��һ�����������۳ɱ�Ϊ20Ԫ/ǧ�˵�ij��Ʒ��������۲��Ź涨���ò�Ʒÿǧ���ۼ۲��ó���90Ԫ�������۹����з��ֵ�����y��ǧ�ˣ����ۼ�x��Ԫ/ǧ�ˣ�����һ�κ�����ϵ����Ӧ��ϵ���±���
�ۼ�x��Ԫ/ǧ�ˣ� | �� | 50 | 60 | 70 | 80 | �� |
������y��ǧ�ˣ� | �� | 100 | 90 | 80 | 70 | �� |
��1����y��x�ĺ�����ϵʽ��
��2����������������4000Ԫ������Ӧ���ۼ۶�Ϊ����Ԫ��
��3���ò�Ʒÿǧ���ۼ�Ϊ����Ԫʱ�������̻�õ�����w��Ԫ�����ʱ���������Ϊ����Ԫ��