题目内容
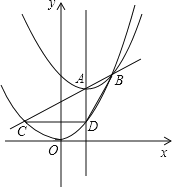
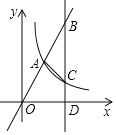
【题目】如图,抛物线y=ax2+bx+c的顶点为D,与x轴交点A,B的横坐标分别为﹣1,3,与y轴负半轴交于点C.下面五个结论:
①2a+b=0;
②4a+2b+c>0;
③对任意实数x,ax2+bx≥a+b;
④只有当a=![]() 时,△ABD是等腰直角三角形;
时,△ABD是等腰直角三角形;
⑤使△ABC为等腰三角形的a值可以有3个.
其中正确的结论有_____.(填序号)
【答案】①③④.
【解析】
先根据图象与x轴的交点A,B的横坐标分别为﹣1,3确定出AB的长及对称轴,再由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:①∵图象与x轴的交点A,B的横坐标分别为﹣1,3,
∴AB=4,
∴对称轴x=﹣![]() =1,
=1,
即2a+b=0;
故①正确,符合题意;
②由图象看,当x=2时,y=4a+2b+c<0,
故②错误,不符合题意;
③函数的对称轴为直线x=1,函数在x=1时,取得最小值,
故ax2+bx+c≥a+b+c,
即ax2+bx≥a+b正确,符合题意;
④要使△ABD为等腰直角三角形,必须保证D到x轴的距离等于AB长的一半;
D到x轴的距离就是当x=1时y的值的绝对值.
当x=1时,y=a+b+c,
即|a+b+c|=2,
∵当x=1时,y<0,
∴a+b+c=﹣2,
又∵图象与x轴的交点A,B的横坐标分别为﹣1,3,
∴当x=﹣1时y=0,即a﹣b+c=0;
当x=3时,y=0.
∴9a+3b+c=0,
解这三个方程可得:b=﹣1,a=![]() ,c=﹣
,c=﹣![]() ,
,
故④正确,符合题意;
⑤要使△ACB为等腰三角形,则必须保证AB=BC=4或AB=AC=4或AC=BC,
当AB=BC=4时,
∵AO=1,△BOC为直角三角形,
又∵OC的长即为|c|,
∴c2=16﹣9=7,
∵由抛物线与y轴的交点在y轴的负半轴上,
∴c=﹣![]() ,
,
与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=![]() ;
;
同理当AB=AC=4时,
∵AO=1,△AOC为直角三角形,
又∵OC的长即为|c|,
∴c2=16﹣1=15,
∵由抛物线与y轴的交点在y轴的负半轴上,
∴c=﹣![]() ,
,
与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=![]() ;
;
同理当AC=BC时
在△AOC中,AC2=1+c2,
在△BOC中BC2=c2+9,
∵AC=BC,
∴1+c2=c2+9,此方程无解.
经解方程组可知只有两个a值满足条件.
故⑤错误.
故答案为:①③④.

 阅读快车系列答案
阅读快车系列答案【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
【题目】一家商店经营一种玩具,进价为每件50元,调查市场发现日销售量y(件)是关于售价x(元/件)的一次函数,相关数据如表,商店每天的总支出是600元.
售价(元/件) | 50 | 55 | 60 | 65 |
日销售量y/件 | 80 | 70 | 60 | 50 |
(1)直接写出y与x之间的函数关系式.(不要求写出自变量x的取值范围)
(2)商店在“五一”这天尽可能优惠顾客,正好收支平衡(收入=支出),问当天玩具的售价为多少元/件.
(3)商店最早需要多少天,纯利可以突破万元,玩具的售价应定为多少元/件?(每天纯利=每天的销售额﹣成本﹣每天的支出)