题目内容
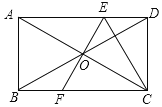
【题目】如图①,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
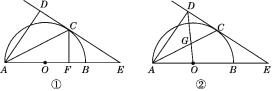
(1)求证:AC平分∠DAB;
(2)若AB=6,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
(3)如图②,连接OD交AC于点G,若![]() =
=![]() ,求cosE的值.
,求cosE的值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)连结OC,如图1,根据切线的性质得OC⊥DE,而AD⊥DE,根据平行线的性质得OC∥AD,所以∠2=∠3,加上∠1=∠3,则∠1=∠2,所以AC平分∠DAB;
(2)如图1,由B为OE的中点,AB为直径得到OB=BE=3,OC=3,在Rt△OCE中,由于OE=2OC,根据含30度的直角三角形三边的关系得∠OEC=30°,则∠COE=60°,由CF⊥AB得∠OFC=90°,所以∠OCF=30°,再根据含30度的直角三角形三边的关系得OF=![]() OC=
OC=![]() ,再由勾股定理即可求出CF的长度;
,再由勾股定理即可求出CF的长度;
(3)连结OC,如图2,先证明△OCG∽△DAG,利用相似的性质得![]() =
=![]() =
=![]() ,再证明△ECO∽△EDA,利用相似比得到
,再证明△ECO∽△EDA,利用相似比得到![]() =
=![]() =
=![]() ,设⊙O的半径为R,OE=x,代入求得OE=3R,最后在Rt△OCE中,根据余弦的定义求解.
,设⊙O的半径为R,OE=x,代入求得OE=3R,最后在Rt△OCE中,根据余弦的定义求解.
(1)证明:连结OC,如图1,

∵DE与⊙O切于点C,
∴OC⊥DE,
∵AD⊥DE,
∴OC∥AD,
∴∠2=∠3,
∵OA=OC,
∴∠1=∠3,
∴∠1=∠2,
即AC平分∠DAB;
(2)∵直径AB=6,B为OE的中点,
∴OB=BE=4,OC=3,
在Rt△OCE中,OE=2OC,
∴∠OEC=30°,
∴∠COE=60°,
∵CF⊥AB,
∴∠OFC=90°,
∴∠OCF=30°,
∴OF==![]() OC=
OC=![]() ,
,
∴由勾股定理可知:CF=![]()
(3)连结OC,如图2,
∵OC∥AD,
∴△OCG∽△DAG,
∴![]() =
=![]() =
=![]() ,
,
∵OC∥AD,
∴△ECO∽△EDA,
∴![]() =
=![]() =
=![]() ,
,
设⊙O的半径为R,OE=x,
∴![]() =
=![]() ,解得OE=x=3R,
,解得OE=x=3R,
在Rt△OCE中,
由勾股定理可知:CE=2√2R,
cos∠E=![]() =
=![]() .
.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
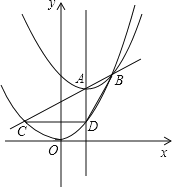
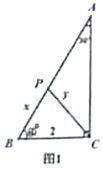
芒果教辅暑假天地重庆出版社系列答案【题目】数学活动课上,小明同学根据学习函数的经验,对函数的图像、性质进行了探究,下面是小明同学探究过程,请补充完整:
如图1,已知在![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的一个动点,连接
边上的一个动点,连接![]() .设
.设![]() ,
,![]() .
.
(初步感知)
(1)当![]() 时,则①
时,则①![]() ________,②
________,②![]() ________;
________;
(深入思考)
(2)试求![]() 与
与![]() 之间的函数关系式并写出自变量
之间的函数关系式并写出自变量![]() 的取值范围;
的取值范围;
(3)通过取点测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 0.5 | 1 | 1.5 | 2. | 2.5 | 3 | 3.5 | 4 |
| 2 | 1.8 | 1.7 | _____ | 2 | 2.3 | 2.6 | 3.0 | _____ |
(说明:补全表格时相关数值保留一位小数)
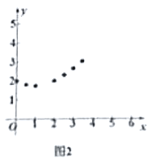
1)建立平面直角坐标系,如图2,描出已补全后的表中各对应值为坐标的点,画出该函数的图象;
2)结合画出的函数图象,写出该函数的两条性质:
①________________________________;②________________________________.
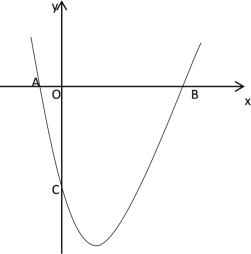
【题目】一家商店经营一种玩具,进价为每件50元,调查市场发现日销售量y(件)是关于售价x(元/件)的一次函数,相关数据如表,商店每天的总支出是600元.
售价(元/件) | 50 | 55 | 60 | 65 |
日销售量y/件 | 80 | 70 | 60 | 50 |
(1)直接写出y与x之间的函数关系式.(不要求写出自变量x的取值范围)
(2)商店在“五一”这天尽可能优惠顾客,正好收支平衡(收入=支出),问当天玩具的售价为多少元/件.
(3)商店最早需要多少天,纯利可以突破万元,玩具的售价应定为多少元/件?(每天纯利=每天的销售额﹣成本﹣每天的支出)