Question

已知抛物线y=x²+bx+c与直线y=x+1有两个交点A、B．
（1）当AB的中点落在y轴时，求c的取值范围；
（2）当AB=2

2

，求c的最小值，并写出c取最小值时抛物线的解析式；
（3）设点P（t，T）在AB之间的一段抛物线上运动，S（t）表示△PAB的面积．
①当AB=2

2

，且抛物线与直线的一个交点在y轴时，求S（t）的最大值，以及此时点P的坐标；
②当AB=m（正常数）时，S（t）是否仍有最大值，若存在，求出S（t）的最大值以及此时点P的坐标（t，T）满足的关系，若不存在说明理由．

Answer 1

（1）由x²+bx+c=x+1，得x²+（b-1）x+c-1=0①．
设交点A（x₁，y₁），B（x₂，y₂） （x₁＜x₂）．
∵AB的中点落在y轴，
∴A，B两点到y轴的距离相等，即A，B两点的横坐标互为相反数，
∴x₁+x₂=0，
故

b-1=0 △=(b-1)2-4(c-1)＞0

∴c＜1；（3分）

（2）∵AB=2

2

，如图，过A作x轴的平行线，过B作y轴的平行线，它们交于G点，
∵直线y=x+1与x轴的夹角为45°，
∴△ABG为等腰直角三角形，
而AB=2

2

，
AG=

2 2

2

=2，
即|x₁-x₂|=2，
∴（x₁+x₂）²-4x₁x₂=4，
由（1）可知x₁+x₂=-（b-1），x₁x₂=c-1．
代入上式得：（b-1）²-4（c-1）=4，
∴c=

1

4

(b-1)2≥0∴c的最小值为0；此时，b=1，c=0，抛物线为y=x2+x；

（3）①∵AB=2

2

由(2)知c=

1

4

(b-1)2成立．
又∵抛物线与直线的交点在y轴时，交点的横坐标为0，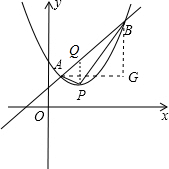
把x=0代入①，得c-1=0，∴c=1．
∴这一交点为（0，1）；
∴

1

4

(b-1)2=1∴b=-1或3；
当b=-1时，y=x²-x+1，过P作PQ∥y轴交直线AB于Q，则有：
P（t，t²-t+1），Q（t，t+1）；
∴PQ=t+1-（t²-t+1）=-t²+2t；
∴S（t）=

1

2

PQ×

2

2

AB=-t²+2t=-（t-1）²+1；
当t=1时，S（t）有最大值，且S（t）_最大=1，此时P（1，1）；
当b=3时，y=x²+3x+1，同上可求得：
S（t）=

1

2

PQ×

2

2

AB=-t²-2t=-（t+1）²+1；
当t=-1时，S（t）有最大值，且S（t）_最大=1，此时P（-1，-1）；
故当P点坐标为（1，1）或（-1，-1）时，S（t）最大，且最大值为1；
②同（2）可得：（b-1）²-4（c-1）=m²，
由题意知：c=1，则有：
（b-1）²=m²，即b=1±m；
当b=1+m时，y=x²+（1+m）x+1，
∴P（t，t²+（1+m）t+1），Q（t，t+1）；
∴PQ=t+1-[t²+（1+m）t+1]=-t²-mt；
∴S（t）=

1

2

PQ×

2

2

AB=

1

2

（-t²-mt）×

2

2

m=-

2

4

m（t+

m

2

）²+

2

16

m³；
∴当t=-

m

2

时，S（t）_最大=

2

16

m³，
此时P（-

1

2

m，-

m2

4

-

m

2

+1）；
当b=1-m时，y=x²+（1-m）x+1，同上可求得：
S（t）=-

2

4

m（t-

m

2

）²+

2

16

m³；
∴当t=

1

2

m时，S（t）_最大=

2

16

m³，
此时P（

1

2

m，

3

4

m2+

1

2

m+1）；
故当P（-

1

2

m，-

m2

4

-

m

2

+1）或（

1

2

m，

3

4

m2+

1

2

m+1）时，S（t）有最大值，且最大值为

2

16

m³．