题目内容

学校大门如图所示是一抛物线形水泥建筑物，大门的地面宽度为8米，两侧距地4米高处各有一挂校名横匾用的铁环，两铁环的水平距离为6米，则该校门的高度（精确到0.1米）为（　　）
A．8.9米B．9.1米C．9.2米D．9.3米

以地面为x轴，大门左边与地面的交点为原点建立平面直角坐标系，

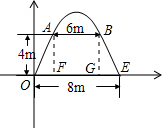
则抛物线过O（0，0）、E（8，0）、A（1、4）、B（7、4）四点，
设该抛物线解析式为：y=ax2+bx+c，
则
c=0
64a+8b+c=0
a+b+c=4
，
解得：
a=-
4
7
b=
32
7
．
故函数解析式为：y=-
4
7
x2+
32
7
x．
当x=4时，可得y=-
64
7
+
128
7
=
64
7
≈9.1米．
故选B．
练习册系列答案
相关题目
如图，已知抛物线y=ax2+bx+c与x轴交于A（1，0），B（3，0）两点，且过点（-1，16），抛物线的顶点是点C，对称轴与x轴的交点为点D，原点为点O．在y轴的正半轴上有一动点N，使以A、O、N这三点为顶点的三角形与以C、A、D这三点为顶点的三角形相似．求：
（1）这条抛物线的解析式；
（2）点N的坐标．
某市举行钓鱼比赛，如图，选手甲钓到了一条大鱼，鱼竿被拉弯近似可看作以A为最高点的一条抛物线，鱼线AB长6m，鱼隐约在水面了，估计鱼离鱼竿支点有8m，此时鱼竿鱼线呈一个平面，且与水平面夹脚α恰好为60°，以鱼竿支点为原点，则鱼竿所在抛物线的解析式为______．
如图，已知直线y=x与抛物线y=
1
2
x2交于A、B两点．
（1）求交点A、B的坐标；
（2）记一次函数y=x的函数值为y1，二次函数y=
1
2
x2的函数值为y2．若y1＞y2，求x的取值范围；
（3）在该抛物线上存在几个点，使得每个点与AB构成的三角形为等腰三角形？并求出不少于3个满足条件的点P的坐标．
如图，抛物线：y=
1
2
x2+bx+c与x轴交于A、B（A在B左侧），顶点为C（1，-2），
（1）求此抛物线的关系式；并直接写出点A、B的坐标．
（2）求过A、B、C三点的圆的半径．
（3）在抛物线上找点P，在y轴上找点E，使以A、B、P、E为顶点的四边形是平行四边形，求点P、E的坐标．
如图，抛物线经过A（-1，0），B（5，0），C（0，-
5
2
）三点．
（1）求抛物线的解析式；
（2）在抛物线的对称轴上有一点P，使PA+PC的值最小，求点P的坐标；
（3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．
如图，抛物线y=
1
2
x2+mx+n交x轴于A、B两点，直线y=kx+b经过点A，与这条抛物线的对称轴交于点M（1，2），且点M与抛物线的顶点N关于x轴对称．
（1）求这条抛物线的函数关系式；
（2）根据图象，写出函数值y为负数时，自变量x的取值范围；
（3）设题中的抛物线与直线的另一交点为C，已知P（x，y）为直线AC上一点，过点P作PQ⊥x轴，交抛物线于点Q．当-1≤x≤1.5时，求线段PQ的最大值．
在△ABC中，∠ACB=90°，点A的坐标为（0，2），点B（-3，1）在抛物线y=ax2+ax-2上，点C在x轴上．
（1）求a的值；
（2）求点C的坐标；
（3）若△ABC是等腰直角三角形
①如图1，将△ABC绕顶点A逆时针方向旋转β°（0＜β＜180°）得到△AB′C′，当点C′（2，1）恰好落在该抛物线上，请你通过计算说明点B′也在该抛物线上．
②如图2，设抛物线与y轴的交点为D、P、Q两点同时从D点出发，点P沿折线D→C→B运动到点B，点Q沿抛物线（在第二、三象限的部分）运动到点B，若P、Q两点的运动速度相同，请问谁先到达点B，为什么？
某校课外活动小组准备利用学校的一面墙，用长为30米的篱笆围成一个矩形生物苗圃园．
（1）若墙长为18米（如图所示），当垂直于墙的一边的长为多少米时，这个苗圃园的面积等于88平方米？
（2）当垂直于墙的一边的长为多少米时，这个苗圃园的面积最大，并求出这个最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网