题目内容
张伯伯利用现有的一面墙(足够长)和60米长的篱笆,把墙外的空地围成四个相连且面积相等的矩形养兔场(如图),设每个小矩形一边的长为x米,设四个小矩形的总面积为y平方米,
(1)请直接写出y与x的函数关系式(不要求写出自变量的取值范围);
(2)当x为何值时,y有最大值,求出最大值.

(1)请直接写出y与x的函数关系式(不要求写出自变量的取值范围);
(2)当x为何值时,y有最大值,求出最大值.

(1)设每个小矩形一边的长为x米,设四个小矩形的总面积为y平方米,
则y=(60-5x)x=-5x2+60x;
(2)∵y=-5x2+60x=-5(x2-12x)=-5(x-6) 2+180,
∴当x=6时,y最大=180.
答:当x为何值6m时,y有最大值,最大值为180平方米.
则y=(60-5x)x=-5x2+60x;
(2)∵y=-5x2+60x=-5(x2-12x)=-5(x-6) 2+180,
∴当x=6时,y最大=180.
答:当x为何值6m时,y有最大值,最大值为180平方米.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
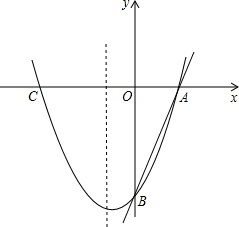
 方向平移1个单位长度后得△AA1B1.
方向平移1个单位长度后得△AA1B1. A(m,0)、B(0,n).
A(m,0)、B(0,n).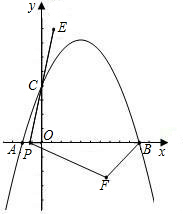 ,(0,2).
,(0,2). 垂直的边AD长为x米,
垂直的边AD长为x米, A、D两点,与抛物线相交于B(1,m)和C(2,2)两点.
A、D两点,与抛物线相交于B(1,m)和C(2,2)两点.