Question

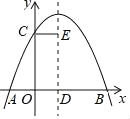
【题目】如图，已知二次函数y＝﹣x2+bx+3的图象与x轴交于A、C两点（点A在点C的左侧），与y轴交于点B，且OA＝OB．

（1）求线段AC的长度；

（2）若点P在抛物线上，点P位于第二象限，过P作PQ⊥AB，垂足为Q．已知PQ＝，求点P的坐标．

Answer 1

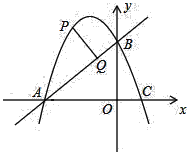
【答案】（1）线段AC的长是4；（2）点P的坐标为（﹣2，3）或（﹣1，4）．

【解析】

（1）根据题意可以求得点B的坐标，从而可得到点A的坐标，进而求得函数解析式，再令y=0，即可得到点C的坐标，从而可以得到线段AC的长；
（2）根据点A和点B的坐标可以得到直线AB的函数解析式，然后根据二次函数的性质和平行线的性质，可以求得点P的坐标，本题得以解决．

（1）∵二次函数y＝﹣x2+bx+3的图象与y轴交于点B，且OA＝OB，

∴点B的坐标为（0，3），∴OB＝OA＝3，

∴点A的坐标为（﹣3，0），∴0＝﹣（﹣3）2+b×（﹣3）+3，解得，b＝﹣2，

∴y＝﹣x2﹣2x+3＝﹣（x+3）（x﹣1），

∴当y＝0时，x1＝﹣3，x2＝1，

∴点C的坐标为（1，0），∴AC＝1﹣（﹣3）＝4，

即线段AC的长是4；

（2）∵点A（﹣3，0），点B（3，0），

∴直线AB的函数解析式为y＝x+3，

过点P作PD∥y轴交直线AB于点D，

设点P的坐标为（m，﹣m2﹣2m+3），则点D的坐标为（m，m+3），

∴PD＝﹣m2﹣2m+3﹣（m+3）＝﹣m2﹣3m，

∵PD∥y轴，∠ABO＝45°，

∴∠PDQ＝∠ABO＝45°，

又∵PQ⊥AB，PQ＝，

∴△PDQ是等腰直角三角形，

∴PD＝＝2，∴﹣m2﹣3m＝2，解得，m1＝﹣1，m2＝﹣2，

当m＝﹣1时，﹣m2﹣2m+3＝4，

当m＝﹣2时，﹣m2﹣2m+3＝3，

∴点P的坐标为（﹣2，3）或（﹣1，4）．