题目内容
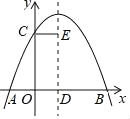
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C,与x轴交于A,B两点,其中点B的坐标为B(4,0),抛物线的对称轴交x轴于点D,CE∥AB,并与抛物线的对称轴交于点E现有下列结论:①b2﹣4a<0;②b>0;③5a+b<0;④AD+CE=4.其中正确结论个数为( )
A. 4 B. 3 C. 2 D. 1
【答案】B
【解析】
根据图象的开口方向、与x和y轴的交点、对称轴所在的位置,判断即可.
抛物线与x轴有两个交点,
∴b2﹣4a>0,故①错误;
该函数图象的开口向下,a<0,-![]() >0,
>0,
∴b>0,故②正确;
∵抛物线y=ax2+bx+c(a≠0)与x轴交于B点,B(4,0),
∴![]()
∴①﹣②得,15a+3b<0,即5a+b<0,故③正确;
∵AD=DB,CE=OD,∴AD+OD=DB+OD=OB=4,可得:AD+CE=4,故④正确.
故选B.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案【题目】“元且”期间,某校组织开展“班际歌泳比赛”,甲、乙班共有学生102人(其中甲班人数多于乙班人数,且甲班人数不够100人)报名统一购买服装参加演出.下面是某服装厂给出的演出服装的价格表:
购买服装的套数 | 1~50 | 51~100 | ≥101 |
每套服装的价格/元 | 70 | 60 | 50 |
如果两班分别单独购买服装,总共要付款6580元
(1)如果甲、乙两班联合起来购买服装,那么比各自购买服装总共可以节省多少钱?
(2)甲、乙班各有多少学生报名参加比赛?
(3)如果甲班有5名学生因特殊情况不能参加演出,请你为两班设计一种省钱的购买服装方案.
【题目】某校为了解同学们课外阅读名著的情况,在八年级随机抽查了20名学生,调查结果如表所示:
课外名著阅读量(本) | 8 | 9 | 10 | 11 | 12 |
学生人数 | 3 | 3 | 4 | 6 | 4 |
关于这20名学生课外阅读名著的情况,下列说法错误的是( )
A.中位数是10B.平均数是10.25C.众数是11D.阅读量不低于10本的同学点70%