题目内容
【题目】如图,点D,E在△ABC的边BC上,连接AD,AE. ①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:(1)①②![]() ③;(2)①③
③;(2)①③![]() ②;(3)②③
②;(3)②③![]() ①.
①.

(1)以上三个命题是真命题的为(直接答题号) ;
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据真命题的定义即可得出结论,
(2)根据全等三角形的判定方法及全等三角形的性质即可证明.
(1)①②③,①③②,②③①;
(2)选择①③②,证明如下:
∵AB=AC,
∴∠B=∠C,
在△ABD和△ACE中,
∵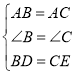 ,
,
∴△ABD≌△ACE(SAS),
∴AD=AE.
选择①②③,证明如下:
∵AB=AC,
∴∠B=∠C,
同理∠ADE=∠AED,
∴180°-∠ADE=180°-∠AED,
即∠ADB=∠AEC,
在△ABD和△ACE中,
∵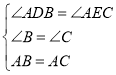 ,
,
∴△ABD≌△ACE,
∴BD=CE.
选择②③①,
∵AD=AE,
∴∠ADE=∠AED,
∴180°-∠ADE=180°-∠AED,
即∠ADB=∠AEC,
在△ABD和△ACE中,
∵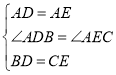 ,
,
∴△ABD≌△ACE,
∴AB=AC.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目