题目内容
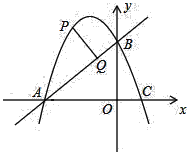
【题目】如图,在Rt△ABC中,![]() ,
,![]() 角平分线交BC于O,以OB为半径作⊙O.(1)判定直线AC是否是⊙O的切线,并说明理由;
角平分线交BC于O,以OB为半径作⊙O.(1)判定直线AC是否是⊙O的切线,并说明理由;
(2)连接AO交⊙O于点E,其延长线交⊙O于点D,![]() ,求
,求![]() 的值;
的值;
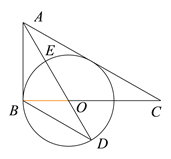
(3)在(2)的条件下,设![]() 的半径为3,求AC的长.
的半径为3,求AC的长.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)由于题目没有说明直线AC与⊙O有交点,所以过点O作OF⊥AC于点F,然后证明OB=OF即可;
(2)连接BE,先求证∠ABE=∠ODB,然后可知△ABE∽△ADB,所以![]() ,而tan∠D=
,而tan∠D=![]() ,于是得到结论;
,于是得到结论;
(3)设![]() 在
在![]() 和
和![]() 中根据
中根据![]() 列二元一次方程组求解即可.
列二元一次方程组求解即可.
详解:(1)AC是⊙O的切线
理由:![]()
![]() ,
,![]()
![]() ,
,
作![]() 于
于![]() ,
,
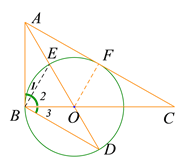
![]()
![]() 是
是![]() 的角平分线,
的角平分线,
![]() ,
,
![]() AC是⊙O的切线
AC是⊙O的切线
(2)连接![]() ,
,
![]()
![]() 是⊙O的直径,
是⊙O的直径,
![]()
![]() ,即
,即![]() .
.
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
又![]()
![]() (同角) ,
(同角) ,
![]()
![]() ∽
∽ ![]() ,
,
![]()
![]()
![]()
(3) 设![]()
在![]() 和
和![]() 中,由三角函数定义有:
中,由三角函数定义有:
![]()
得: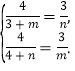
解之得:![]()
![]()
![]() 即
即![]() 的长为
的长为![]()

【题目】“元且”期间,某校组织开展“班际歌泳比赛”,甲、乙班共有学生102人(其中甲班人数多于乙班人数,且甲班人数不够100人)报名统一购买服装参加演出.下面是某服装厂给出的演出服装的价格表:
购买服装的套数 | 1~50 | 51~100 | ≥101 |
每套服装的价格/元 | 70 | 60 | 50 |
如果两班分别单独购买服装,总共要付款6580元
(1)如果甲、乙两班联合起来购买服装,那么比各自购买服装总共可以节省多少钱?
(2)甲、乙班各有多少学生报名参加比赛?
(3)如果甲班有5名学生因特殊情况不能参加演出,请你为两班设计一种省钱的购买服装方案.
【题目】某校为了解同学们课外阅读名著的情况,在八年级随机抽查了20名学生,调查结果如表所示:
课外名著阅读量(本) | 8 | 9 | 10 | 11 | 12 |
学生人数 | 3 | 3 | 4 | 6 | 4 |
关于这20名学生课外阅读名著的情况,下列说法错误的是( )
A.中位数是10B.平均数是10.25C.众数是11D.阅读量不低于10本的同学点70%