题目内容
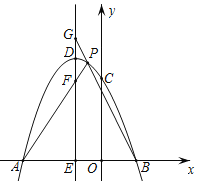
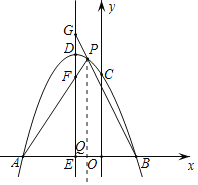
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A、B两点(A在B的左侧),且OA=3,OB=1,与y轴交于C(0,3),抛物线的顶点坐标为D(﹣1,4).
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)过点D作直线DE∥y轴,交x轴于点E,点P是抛物线上B、D两点间的一个动点(点P不与B、D两点重合),PA、PB与直线DE分别交于点F、G,当点P运动时,EF+EG是否为定值?若是,试求出该定值;若不是,请说明理由.
【答案】(1)A点坐标(﹣3,0),B点坐标(1,0);(2)抛物线的解析式为y=﹣x2﹣2x+3;(3)EF+EG=8(或EF+EG是定值),理由见解析.
【解析】(1)根据OA,OB的长,可得答案;
(2)根据待定系数法,可得函数解析式;
(3)根据相似三角形的判定与性质,可得EG,EF的长,根据整式的加减,可得答案.
(1)由抛物线y=ax2+bx+c交x轴于A、B两点(A在B的左侧),且OA=3,OB=1,得
A点坐标(﹣3,0),B点坐标(1,0);
(2)设抛物线的解析式为y=a(x+3)(x﹣1),
把C点坐标代入函数解析式,得
a(0+3)(0﹣1)=3,
解得a=﹣1,
抛物线的解析式为y=﹣(x+3)(x﹣1)=﹣x2﹣2x+3;
(3)EF+EG=8(或EF+EG是定值),理由如下:
过点P作PQ∥y轴交x轴于Q,如图,
设P(t,﹣t2﹣2t+3),
则PQ=﹣t2﹣2t+3,AQ=3+t,QB=1﹣t,
∵PQ∥EF,
∴△AEF∽△AQP,
∴![]() ,
,
∴EF=![]() =
=![]() ;
;
又∵PQ∥EG,
∴△BEG∽△BQP,
∴![]() ,
,
∴EG=![]() =
=![]() =2(t+3),
=2(t+3),
∴EF+EG=2(1﹣t)+2(t+3)=8.

 阅读快车系列答案
阅读快车系列答案【题目】为了参加“荆州市中小学生首届诗词大会”,某校八年级的两班学生进行了预选,其中班上前5名学生的成绩(百分制)分别为:八(1)班86,85,77,92,85;八(2)班79,85,92,85,89.通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 | 方差 |
八(1) | 85 | b | c | 22.8 |
八(2) | a | 85 | 85 | 19.2 |
(1)直接写出表中a,b,c的值;
(2)根据以上数据分析,你认为哪个班前5名同学的成绩较好?说明理由.