题目内容
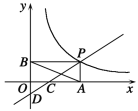
【题目】如图，直线
与x轴、y轴分别交于C、D两点，与双曲线
在第一象限内交于点P，过点P作PA⊥x轴于点A，PB⊥y轴于点B，已知B（0，4）且S△DBP=27.
（1）直接写出直线的解析式_____________，双曲线的解析式____________；
（2）设点Q是直线上的一点，且满足△DOQ的面积是△COD面积的2倍，请求出点Q的坐标；
【答案】（1）
；
；（2）点Q的坐标 （6，2）或（－6，－6）.
【解析】
（1）令一次函数解析式中x=0，求出对应的y值，确定出D的坐标，得到OD的长，再由已知条件得到OB的长，由OD+OB求出BD的长，在直角三角形BDP中，利用两直角边乘积的一半表示出三角形的面积，将BD及已知的面积代入求出BP的长，确定出P的坐标，由P为一次函数与反比例函数的交点，将P的坐标代入一次函数解析式中求出k的值，确定出一次函数解析式，将P的坐标代入反比例函数解析式中求出m的值，确定出反比例函数解析式；
（2）先求得C的坐标，进而根据S△DOQ=2S△COD，求得MQ=2OC=6，然后分两种情况讨论求得．
（1）∵一次函数y=kx-2的图象交y轴于点D，
∴OD=2．
∵B（0，4），
∴BD=2+4=6，
∵S△DBP=27，
∴
BDBP=27，
∴BP=9，
∴P（9，4）；
把点P的坐标代入y=kx-2得：k=
，
∴一次函数的解析式为：y=x-2，
把点P的坐标代入y=
得：m=36．
∴反比例函数的表达式是y=
；
（2）∵直线交x轴于点C，
∴点C的坐标是（3，0），OC=3.
过点Q作QM⊥y轴于点M.
分为以下两种情况：
①当点Q在射线DC上时，
∵△DOQ的面积是△COD面积的2倍，且△DOQ和△COD有共同的底边OD，
∴MQ=2OC=6.
把x=6代入，得y=2，
即此时点Q的坐标是（6，2）.
②当点Q在射线CD上时，同理可得QM=6，
把x=－6代入，得y=－6，
即此时点Q的坐标是（－6，－6）.
∴点Q的坐标 （6，2）或（－6，－6）.
