题目内容
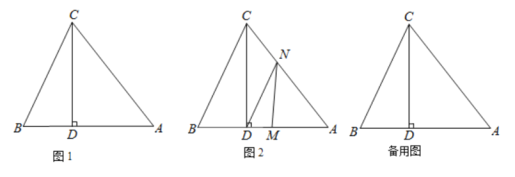
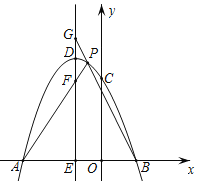
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.
(1)如图1,点E,F在AB,AC上,且∠EDF=90°.求证:BE=AF;
(2)点M,N分别在直线AD,AC上,且∠BMN=90°.
①如图2,当点M在AD的延长线上时,求证:AB+AN=![]() AM;
AM;
②当点M在点A,D之间,且∠AMN=30°时,已知AB=2,直接写出线段AM的长.

【答案】(1)证明见解析;(2)①证明见解析;②AM=![]() .
.
【解析】(1)先判断出∠BAD=∠CAD=45°,进而得出∠CAD=∠B,再判断出∠BDE=∠ADF,进而判断出△BDE≌△ADF,即可得出结论;
(2)①先判断出AM=PM,进而判断出∠BMP=∠AMN,判断出△AMN≌△PMB,即可判断出AP=AB+AN,再判断出AP=![]() AM,即可得出结论;
AM,即可得出结论;
②先求出BD,再求出∠BMD=60°,最后用三角函数求出DM,即可得出结论.
(1)∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°.
∵AD⊥BC,
∴BD=CD,∠BAD=∠CAD=45°,
∴∠CAD=∠B,AD=BD.
∵∠EDF=∠ADC=90°,
∴∠BDE=∠ADF,
∴△BDE≌△ADF(ASA),
∴DE=DF;
(2)①如图1,过点M作MP⊥AM,交AB的延长线于点P,
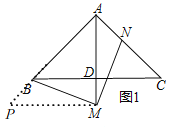
∴∠AMP=90°.
∵∠PAM=45°,
∴∠P=∠PAM=45°,
∴AM=PM.
∵∠BMN=∠AMP=90°,
∴∠BMP=∠AMN.
∵∠DAC=∠P=45°,
∴△AMN≌△PMB(ASA),
∴AN=PB,
∴AP=AB+BP=AB+AN.
在Rt△AMP中,∠AMP=90°,AM=MP,
∴AP=![]() AM,
AM,
∴AB+AN=![]() AM;
AM;
②在Rt△ABD中,AD=BD=![]() AB=
AB=![]() .
.
∵∠BMN=90°,∠AMN=30°,
∴∠BMD=90°﹣30°=60°.
在Rt△BDM中,DM=![]() =
=![]() ,
,
∴AM=AD﹣DM=![]() ﹣
﹣![]() .
.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案