��Ŀ����
����Ŀ��A��B��CΪ�����ϵ����㣬����A��Bͬʱ��ԭ�����������Aÿ���˶�x����λ������Bÿ���˶�y����λ���Ҷ���A�˶�����λ�ö�Ӧ������Ϊa������B�˶�����λ�ö�Ӧ������Ϊb������C��Ӧ����Ϊ8��
��1����2���a��b����|a+8|+|b��2|��0����x���� ����y���� ���������������ϱ��A��B�����λ�ã�
��2��������A��B�ڣ�1���˶����λ���ϱ���ԭ�����ٶȣ���ͬʱ���������˶�z���ʹ��|a|��|b|��ʹ��z���� ����
��3��������A��B�ڣ�1���˶����λ���϶���ÿ��2����λ���������˶������˶�t�룬��A���C֮��ľ����ʾΪAC����B���C֮��ľ����ʾΪBC����A���B֮��ľ���ΪAB����AC+BC��1.5AB����t���� ����
![]()
���𰸡���1��4��1��ͼ�����������2��![]() ��
��![]() ����3��
����3��![]() ��
��![]() ��
��
��������
��1����|a+8|+��b��2��2=0��
��a+8=0��b��2=0����a=��8��b=2��
��x=|��8|��2=4��y=2��2=1��
�������ϱ��A��B�����λ������ͼ��ʾ��
![]()
�ʴ�Ϊ��4��1��
��2���߶���A��B�ڣ�1���˶����λ���ϱ���ԭ�����ٶȣ���ͬʱ���������˶�z���
��a=��8+4z��b=2+z��
��|a|=|b|��
��|��8+4z|=|2+z|��
�ੁ8+4z+2+z=0��8+4z=2+z
��ã�z=![]() ��z=
��z=![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��
��3��������A��B�ڣ�1���˶����λ���϶���ÿ��2����λ���������˶������˶�t���
���A��ʾ����8+2t����B��ʾ��2+2t����C��ʾ��8��
��AC=|��8+2t��8|=|2t��16|��BC=|2+2t��8|=|2t��6|��AB=|��8+2t����2+2t��|=10��
��AC+BC=1.5AB��
��|2t��16|+|2t��6|=1.5��10��
������������ۣ�
�ٵ�t��3ʱ��
16-2t+6-2t=15��
��ã�t=![]() ��
��
�ڵ�3��t��8ʱ��
16-2t+2t-6=10��15
�����⣻
�۵�t��8ʱ��
2t-16+2t-6=15
��ã�t=![]() ��
��
����������t=![]() ��t=
��t=![]() ��
��
�ʴ�Ϊ��![]() ��
�� ![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��̽������y=x+![]() ��x��0����y=x+
��x��0����y=x+![]() ��x��0��a��0����������ʣ�
��x��0��a��0����������ʣ�
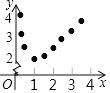
��1��С��ͬѧ�Ժ���y=x+![]() ��x��0�������������б�����㣬�������������ߵIJ��裻�۲�ͼ��ɵ�������СֵΪ�� ����������һ������Ϊ�� ����
��x��0�������������б�����㣬�������������ߵIJ��裻�۲�ͼ��ɵ�������СֵΪ�� ����������һ������Ϊ�� ����
x | �� |
|
|
| 1 |
| 2 |
| 3 | �� |
y | �� |
|
|
| 2 |
|
|
|
| �� |
��2�������䷽������y=x+![]() ��x��0������Сֵ��
��x��0������Сֵ��
��3�����뺯��y=x+![]() ��x��0��a��0������СֵΪ�� ����
��x��0��a��0������СֵΪ�� ����