题目内容
【题目】(1)问题发现:如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,则∠AEB的度数为 ,线段AD、BE之间的关系 .
(2)拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.①请判断∠AEB的度数,并说明理由;②当CM=5时,AC比BE的长度多6时,求AE的长.

【答案】(1)60°;相等;(2)①∠AEB=90°;②AE= 17.
【解析】
(1)易证∠ACD=∠BCE,即可求证△ACD≌△BCE,根据全等三角形对应边相等可求得AD=BE,根据全等三角形对应角相等即可求得∠AEB的大小;
(2)易证△ACD≌△BCE,利用勾股定理进行解答即可.
解:(1)∵∠ACB=∠DCE,∠DCB=∠DCB,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
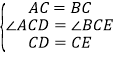 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CEB=∠ADC=180°﹣∠CDE=120°,
∴∠AEB=∠CEB﹣∠CED=60°,
故答案为:60°;相等;
(2)①∠AEB=90°,
∵△ACB和△DCE均为等腰直角三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=90°,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
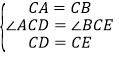 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠ADC=∠BEC.
∵△DCE为等腰直角三角形,
∴∠CDE=∠CED=45°,
∵点A、D、E在同一直线上,
∴∠ADC=135°.
∴∠BEC=135°,
∴∠AEB=∠BEC﹣∠CED=90°.
②∵CD=CE,CM⊥DE,
∴DM=ME=5.
在Rt△ACM中,AM2+CM2=AC2,
设:BE=AD=x,则AC=(6+x),
(x+5)2+52=(x+6)2,
解得:x=7.
所以可得:AE=AD+DM+ME=17.



