Question

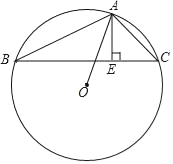
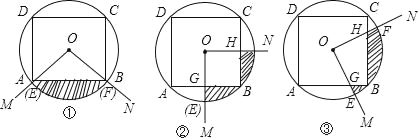
【题目】如图，正方形ABCD内接于⊙O，圆心O是正方形的对称中心，⊙O的面积为S1，正方形的面积为S2，则以圆心O为顶点，作∠MON=90°，将∠MON绕O点旋转，OM、ON分别与⊙O交于E、F，分别于正方形ABCD交于G、H，设由OE、OF、EF及正方形ABCD的边围成的图形（阴影部分）的面积为S，那么：

（1）如图①，当OM经过点A时，S、S1、S2之间的关系（用S1、S2的代数式表示S）为　 　；

（2）如图②，当OM⊥AB交于点G时，①中的结论还成立吗？并说明理由；

（3）如图③，∠MON旋转到任意位置时，则①中的结论是否仍然成立？若成立，请证明；若不成立，请说明理由．

Answer 1

【答案】（1）；（2）成立；（3）成立.

【解析】

（1）如图①，利用正方形的性质得到∠AOB=90°，则可判断OM经过点A时，ON经过点B，根据扇形的面积公式，利用S=S扇形EOF﹣S△AOB得到S=（S1﹣S2）；

（2）如图②，先证明ON⊥BC，利用S=S扇形EOF﹣S矩形OGBH得到S=（S1﹣S2），从而判断（1）的结论成立；

（3）如图③，连接OB、OA，先证明∠AOE=∠BOH，则判断△AOG≌△BOH，从而得到S△AOG=S△BOH，所以S四边形OGBH=S△AOB，然后利用S=S扇形EOF﹣S四边形OGBH=S扇形EOF﹣S△AOB得到S=（S1﹣S2），于是可判断（1）中的结论成立．

（1）如图①．

∵正方形ABCD内接于⊙O，圆心O是正方形的对称中心，∴∠AOB=90°．

∵∠MON=90°，∴OM经过点A时，ON经过点B，∴S=S扇形EOF﹣S△AOB=S1﹣S2=（S1﹣S2）．

故答案为：（S1﹣S2）；

（2）成立．理由如下：

如图②，当OM⊥AB交于点G时．

∵∠ABC=90°，∠GOH=90°，∴∠OHB=90°，∴ON⊥BC，∴S=S扇形EOF﹣S矩形OGBH=S1﹣S2=（S1﹣S2）；

（3）成立．理由如下：

如图③，连接OB、OA．

∵四边形ABCD为正方形，∴OA=OB，∠OAB=∠OBC=45°．

∵∠AOB=90°，∠EOF=90°，∴∠AOE=∠BOH．在△AOG和△BOH中，∵

，∴△AOG≌△BOH，∴S△AOG=S△BOH，∴S四边形OGBH=S△AOB，∴S=S扇形EOF﹣S四边形OGBH=S扇形EOF﹣S△AOB=S1﹣S2=（S1﹣S2）．