题目内容
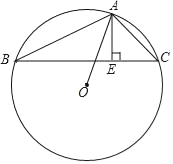
【题目】如图，在钝角△ABC中，∠C=45°，AE⊥BC，垂足为E点，且AB与AC的长度为方程x2﹣9x+18=0的两个根，⊙O是△ABC的外接圆．
求：（1）⊙O的半径；
（2）BE的长．
【答案】（1）OB =3
；（2）BE=
．
【解析】
（1）连接OB，解方程求出AC、AB，根据勾股定理求出半径；
（2）根据题意得到△AEC为等腰直角三角形，根据勾股定理计算即可．
解：（1）连接OB，
解方程x2﹣9x+18=0，
得，x1=3，x2=6，
由图形可知，AC=3，AB=6，
由圆周角定理得，∠AOB=2∠C=90°，
∴△AOB为等腰直角三角形，
∴OB=
AB=3
；
（2）∵∠C=45°，AE⊥BC，
∴△AEC为等腰直角三角形，
∴AE=AC=
，
∴BE=
=
．
天天向上一本好卷系列答案
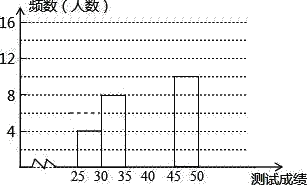
小学生10分钟应用题系列答案
【题目】为了提高学生书写汉字的能力，增强保护汉字的意识，我市举办了首届“汉字听写大赛”，经选拔后有50名学生参加决赛，这50名学生同时听写50个汉字，若每正确听写出一个汉字得1分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：
组别 | 成绩x分 | 频数（人数） |
第1组 | 25≤x＜30 | 4 |
第2组 | 30≤x＜35 | 8 |
第3组 | 35≤x＜40 | 16 |
第4组 | 40≤x＜45 | a |
第5组 | 45≤x＜50 | 10 |
请结合图表完成下列各题：
（1）求表中a的值；
（2）请把频数分布直方图补充完整；
（3）若测试成绩不低于40分为优秀，则本次测试的优秀率是多少？
（4）第5组10名同学中，有4名男同学，现将这10名同学平均分成两组进行对抗练习，且4名男同学每组分两人，求小宇与小强两名男同学能分在同一组的概率．
【题目】为“厉行节能减排，倡导绿色出行”，某公司拟在我县甲、乙两个街道社区试点投放一批共享单车（俗称“小黄车”），这批自行车包括A、B两种不同款型，投放情况如下表：
成本单价 （单位：元） | 投放数量（单位：辆） | 总价（单位：元） | |
A型 |
| 50 | 50 |
B型 |
| 50 |
|
成本合计（单位：元） | 7500 | ||
（1）根据表格填空：
本次试点投放的A、B型“小黄车”共有 辆；用含有
的式子表示出B型自行车的成本总价为 ；
（2）试求A、B两种款型自行车的单价各是多少元？
（3）经过试点投放调查，现在该公司决定采取如下方式投放A型“小黄车”：甲街区每100人投放n辆，乙街区每100人投放（n+2）辆，按照这种投放方式，甲街区共投放1500辆，乙街区共投放1200辆，如果两个街区共有
人，求甲街区每100人投放A型“小黄车”的数量．