��Ŀ����
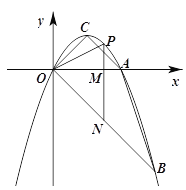
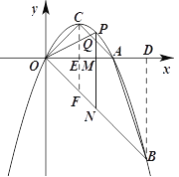
����Ŀ����ͼ��������y��ax2��bx����A��2��0����B��3����3�����㣬�����ߵĶ���ΪC������P��ֱ��OB�Ϸ����������ϣ�����P��ֱ��PM��y�ᣬ��x����M����OB��N�����P�ĺ�����Ϊm��
��1���������ߵĽ���ʽ����C��������
��2������PONΪ����������ʱ����N������Ϊ ������PMO����COBʱ����P������Ϊ ����ֱ��д�������
��3��ֱ��PN�ܷ��ı���ABOC��Ϊ�����Ϊ1��2�������֣����ܣ������m��ֵ�������ܣ���˵�����ɣ�
���𰸡���1�������ߵĽ���ʽΪy����x2��2x��C��1��1������2��N1��1����1����N2��2����2����N3��![]() ��
�� ![]() ��P1��
��P1��![]() ��
�� ![]() ����P2��
����P2��![]() ��
�� ![]() ������3��
������3��![]() ��
��![]()
����������1���������ȸ���������y=ax2+bx��a��0��������2��0��B��3��-3�����㣬�ֱ����a��b��ֵ���ٴ���������y=ax2+bx����������Ľ���ʽ��
��2���ɡ�PONΪ���������ε�����������д����N����P�����ꣻ
��3����BD��x����D����CE��x����E����OB��F����������������OE��EF��Ȼ��ּ�������õ�m ��ֵ��
�⣺��1���������⣬��![]() ��������������
��������������![]()
�������ߵĽ���ʽΪy����x2��2x
��x��![]() ʱ��y����x2��2x��1����C��1��1��
ʱ��y����x2��2x��1����C��1��1��
��2��N1��1����1����N2��2����2����N3��![]() ��
�� ![]() ��
��
P1��![]() ��
�� ![]() ����P2��
����P2��![]() ��
�� ![]() ��
��
��3����BD��x����D����CE��x����E����OB��F
��BD��OD��3��CE��OE��1��OC��AC
���ODB����OCE����AOC��Ϊ����ֱ��������
![]()
���AOC����AOB����OAC��45��
��PM��y�ᣬ��OM��PN����MNO����AOB��45�㣬��OM��MN��m��OE��EF��1
�١�![]()
�൱0��m��1ʱ��������������
�ڵ�1��m��2ʱ����PN��AC��Q����MQ��MA��2��m
![]()
��![]() ����
����![]() �����
�����![]()
![]() ����������
����������
��![]() ����
����![]() �����
�����![]()
![]() ����������
����������
�۵�2��m��3ʱ����AG��x�ᣬ��OB��G��
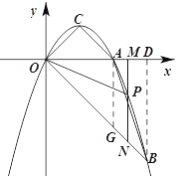
��AG��OA��2��AD��1
��![]()
�൱2��m��3ʱ��������������
��![]() ��
��![]()
���㾦���������ڶ��κ����ۺ��⣬�漰�˴���ϵ������������ʽ��һԪһ�η��̵Ľ⼰�����ε�������ۺ��Խ�ǿ���������ѵ��ڵ����ʣ��ؼ��Ǹ���������з�����⣬�ѶȽϴ�һ����������ѹ���⣮