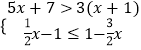题目内容
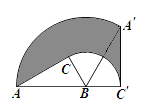
【题目】如图，在△ABC中，AC＝3cm，∠ACB＝90°，∠ABC＝60°，将△ABC绕点B顺时针旋转至△A′BC′，点C′在直线AB上，则边AC扫过区域（图中阴影部分）的面积为____________cm2．
【答案】3π
【解析】易得整理后阴影部分面积为圆心角为120°，两个半径分别为
和2
的圆环的面积．
解：∵在△ABC中，AC＝3cm，∠ACB＝90°，∠ABC＝60°，
∴BC=
，AB=2
，∠A′BA=120°，∠CBC′=120°，
∴阴影部分面积=（S△A′BC′+S扇形BAA′）-S扇形BCC′-S△ABC=
×[（2
）2-（
）2]=3πcm2．
“点睛”本题利用了直角三角形的性质，扇形的面积公式求解．关键是理解AC边扫过的图形中阴影部分的面积是一个环形的面积，然后利用扇形的面积公式求即可．
练习册系列答案
阅读快车系列答案
相关题目
