题目内容
【题目】如图，在四边形ABCD中，AB= 
，AD=1，BC=CD= 
，且∠BCD=90°，试求四边形ABCD的面积．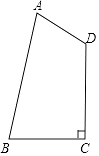 
【答案】解：如图，连接BD，在△ACD中，∠BCD=90°， 由勾股定理得：BD2=CD2+BC2=2．
在△ADB中，∵AD2+BD2=AB2 ．
由勾股定理的逆定理得：∠ADB=90°，则△ADB是直角三角形，
∴S四边形ABCD=S△ABD+S△BCD
= 
ADAB+ BCCD=2
即四边形ABCD的面积是2．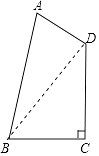
【解析】如图，连接BD．构建直角△ABD、直角△BCD，则四边形ABCD的面积等于图中两直角三角形的面积之和．
【考点精析】利用勾股定理的概念对题目进行判断即可得到答案，需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．
练习册系列答案
相关题目
【题目】园林部门用3600盆甲种花卉和2900盆乙种花卉搭配A、B两种园艺造型共50个，挂放在迎宾大道两侧，搭配每个造型所要花盆数如表，综合上述信息，解答下列问题．
造型 | 甲 | 乙 |
A | 90盆 | 30盆 |
B | 40盆 | 100盆 |
（1）符合题意的搭配方案有哪几种？
（2）若搭配一个A种造型的成本为1000元，搭配一个乙种造型的成本为1200元，选（1）中那种方案的成本最低？
