题目内容
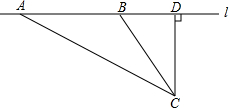
如图,在△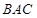 中,
中,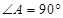 ,
,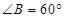 ,作
,作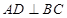 ,垂足为
,垂足为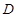 ,
,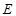 为边
为边 上一点,联结
上一点,联结 交
交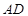 于点
于点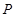 ,点
,点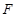 为线段
为线段 上一点,且
上一点,且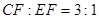 ,联结
,联结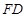 .
.
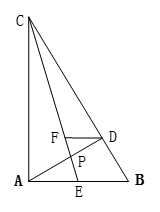
(1)求证: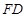 ∥
∥ ;(2)当
;(2)当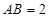 ,且
,且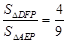 时,求
时,求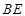 的长.
的长.
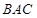 中,
中,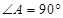 ,
,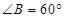 ,作
,作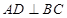 ,垂足为
,垂足为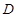 ,
,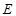 为边
为边 上一点,联结
上一点,联结 交
交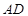 于点
于点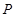 ,点
,点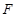 为线段
为线段 上一点,且
上一点,且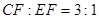 ,联结
,联结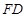 .
.
(1)求证:
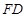 ∥
∥ ;(2)当
;(2)当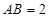 ,且
,且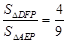 时,求
时,求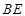 的长.
的长.(2)

试题分析:(1)由题意可知
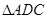 与
与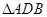 ,均为含有
,均为含有 的直角三角形,所以
的直角三角形,所以 ,
, 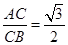
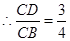 ,因为
,因为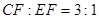 ,即
,即
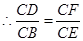 ,
,
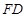 ∥
∥ ;
;(2)根据
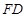 ∥
∥ ,
,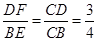 ,同时根据
,同时根据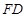 ∥
∥ ,可得
,可得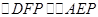 ,由
,由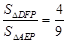 利用相似三角形的面积之比等于相似比的平方,可得
利用相似三角形的面积之比等于相似比的平方,可得 ,所以
,所以 ,即
,即 .
.试题解析:(1)在
 中,∵
中,∵ ,
,∴设
 ,则
,则 (1分)
(1分)在
 中,
中,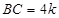
∴
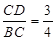 (2分)
(2分)又∵
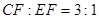 ,∴
,∴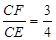 (1分)
(1分)∴
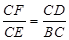 (1分)
(1分)∴
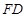 ∥
∥ (1分)
(1分)(也可利用相似三角形来求出
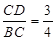 )
)(2)∵
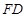 ∥
∥ , ∴△
, ∴△ ∽△
∽△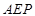 (1分)
(1分)∴
 , ∴
, ∴ (1分)
(1分)由(1)得
 ,即
,即 (1分)
(1分)设
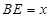 ,
,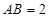 ,则
,则 ,
, ∴
 (1分)
(1分)∴
 ,即
,即 (2分)
(2分)
练习册系列答案
相关题目
 );
);

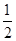 B.
B.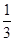 C.
C. D.
D.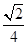



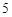

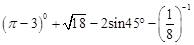 .
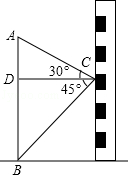
.
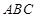 中,
中,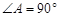 ,如果
,如果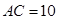 ,
,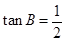 ,那么
,那么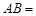 .
.