题目内容
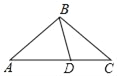
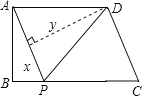
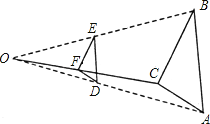
【题目】如图,△ABC纸片中,AB=BC>AC,点D是AB边的中点,点E在边AC上,将纸片沿DE折叠,使点A落在BC边上的点F处.则下列结论成立的个数有( )①△BDF是等腰直角三角形;②∠DFE=∠CFE;③DE是△ABC的中位线;④BF+CE=DF+DE.
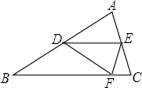
A. 1个B. 2个C. 3个D. 4个
【答案】B
【解析】
根据题意可知△DFE是△DAE对折的图形,所以全等,故AD=DF,而AD=BD,所以BD=DF,但是∠B不一定等于45°,所以△BDF不一定是等腰直角三角形,①不成立;结合①中的结论,BD=DF,而∠ADE=∠FDE,∠ADF=∠DBF+∠DFB,可证∠BFD=∠EDF,故DE∥BC,即DE是△ABC的中位线,③成立;若③成立,利用△ADE≌△FDE,DE∥BC,∠AEF=∠EFC+∠ECF,可证∠DFE=∠CFE,②成立;根据折叠以及中位线定理得右边=AB,要和左边相等,则需CE=CF,则△CEF应是等边三角形,显然不一定,故④不成立.
解:①根据折叠知AD=DF,所以BD=DF,即一定是等腰三角形.因为∠B不一定等于45°,所以①错误;
②连接AF,交DE于G,根据折叠知DE垂直平分AF,又点D是AB边的中点,在△ABF中,根据三角形的中位线定理,得DG∥BF.进一步得E是AC的中点.由折叠知AE=EF,则EF=EC,得∠C=∠CFE.又∠DFE=∠A=∠C,所以∠DFE=∠CFE,正确;
③在②中已证明正确;
④根据折叠以及中位线定理得右边=AB,要和左边相等,则需CE=CF,则△CEF应是等边三角形,显然不一定,错误.
故选:B.

【题目】某校积极参与垃圾分类活动,以班级为单位收集可回收的垃圾,下面是七年级各班一周收集的可回收垃圾的质量频数表和频数直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的质量频数表
组别(kg) | 频数 |
4.0~4.5 | 2 |
4.5~5.0 | a |
5.0~5.5 | 3 |
5.5~6.0 | 1 |
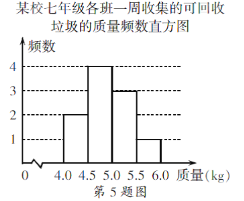
(1)求a的值;
(2)已知收集的可回收垃圾以0.8元/kg被回收,该年级这周收集的可回收垃圾被回收后所得的金额能否达到50元.
【题目】某商场有一个可以自由转动的圆形转盘(如图).规定:顾客购物100元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据:
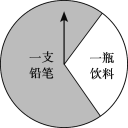
转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 546 | 701 |
落在“铅笔”的频率 (结果保留小数点后两位) | 0.68 | 0.74 | 0.68 | 0.69 | 0.68 | 0.70 |
(1)转动该转盘一次,获得铅笔的概率约为_______;(结果保留小数点后一位)
(2)铅笔每只0.5元,饮料每瓶3元,经统计该商场每天约有4000名顾客参加抽奖活动,请计算该商场每天需要支出的奖品费用;
(3)在(2)的条件下,该商场想把每天支出的奖品费用控制在3000元左右,则转盘上“一瓶饮料”区域的圆心角应调整为______度.