题目内容
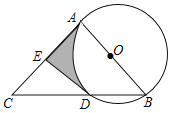
【题目】如图，AB是⊙O的直径，AC是⊙O的切线，切点为A，BC交⊙O于点D，点E是AC的中点．
（1）试判断直线DE与⊙O的位置关系，并说明理由；
（2）若⊙O的半径为3，∠ACB=40°，AC=7.2，求图中阴影部分的周长．
【答案】（1）相切，见解析；（2）
+7.2
【解析】
（1）连接OD，AD,通过圆周角定理的推论得出
，从而有
，再利用直角三角形斜边中线的性质和等腰三角形的性质得出
，
，再根据切线的性质得出
，通过等量代换可得 
，即
，则直线DE与⊙O相切；
（2）阴影部分的周长为
的弧长以及AE+DE的长度和，分别求出求和即可．
（1）直线DE与⊙O相切，理由如下：
连接OD，AD,
∵AB是⊙O的直径，
，
．
∵点E是AC的中点，
，
．
，
．
∵AC是⊙O的切线，
，
，
，
即
，
∴直线DE与⊙O相切；
（2）由（1）知，
，
．
，
，
，
的长为
，
∴阴影部分的周长为
．
练习册系列答案
导学教程高中新课标系列答案
相关题目
【题目】九年级数学兴趣小组经过市场调查，得到某种运动服每月的销量是售价的一次函数，且相关信息如下表：
售价（元/件） | 100 | 110 | 120 | 130 | … |
月销量（件） | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元，设售价为x元．
（1）请用含x的式子表示：①销售该运动服每件的利润是（ ）元；
（2）求月销量y与售价x的一次函数关系式：
（3）设销售该运动服的月利润为W元，那么售价为多少元时，当月的利润最大？最大利润是多少元？
