题目内容
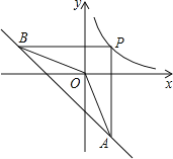
【题目】 如图，一次函数y=2x与反比例函数y=
(k＞0)的图象交于A、B两点，点P在以C(-2，0)为圆心，1为半径的圆上，Q是AP的中点
（1）若AO=
，求k的值；
（2）若OQ长的最大值为
，求k的值；
（3）若过点C的二次函数y=ax2+bx+c同时满足以下两个条件：①a+b+c=0；②当a≤x≤a+1时，函数y的最大值为4a，求二次项系数a的值．
【答案】（1）2；（2）
；（3）a的值为-3或2或-4或1．
【解析】
（1）设A(m，n)，根据勾股定理和一次函数图象上点的坐标特征得出
，解方程组即可求得A的坐标，代入y=
可求得k的值；
（2）作辅助线，先确定OQ长的最大时，点P的位置，当BP过圆心C时，BP最长，设B(t，2t)，则CD=t-(-2)=t+2，BD=-2t，根据勾股定理计算t的值，可得k的值；
（3）根据题意写出抛物线的解析式为：y=ax2+ax-2a=a(x+
)2-
a，即可判定-在a≤x≤a+1范围外，故存在两种可能，即当x=a时，有最大值4a，或x=a+1时有最大值4a，分别代入求得即可．
（1）设A(m，n)，
∵AO=
，
∴m2+n2=5，
∵一次函数y=2x的图象经过A点，
∴n=2m，
∴m2+(2m)2=5，解得m=±1，
∵A在第一象限，
∴m=1，
∴A(1，2)，
∵点A在反比例函数y=(k＞0)的图象上，
∴k=1×2=2；
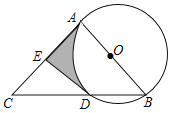
（2）如图，连接BP，
由对称性得：OA=OB，
∵Q是AP的中点，
∴OQ=BP，
∵OQ长的最大值为
，
∴BP长的最大值为×2=3，
如图2，当BP过圆心C时，BP最长，过B作BD⊥x轴于D，
∵CP=1，
∴BC=2，
∵B在直线y=2x上，
设B(t，2t)，则CD=t-(-2)=t+2，BD=-2t，
在Rt△BCD中，由勾股定理得：BC2=CD2+BD2，
∴22=(t+2)2+(-2t)2，
t=0(舍)或-
，
∴B(-，-
)，
∵点B在反比例函数y=(k＞0)的图象上，
∴k=-×(-)=
；
（3）∵抛物线经过点C(-2，0)，
∴4a-2b+c=0，
又∵a+b+c=0，
∴b=a，c=-2a，
∴y=ax2+ax-2a=a(x+)2-a，
∵-＜a≤x≤a+1或a≤x≤a+1＜-，
当x=a时，取得最大值4a，
则aa2+aa-2a=4a，
解得a=-3或2，
当x=a+1时，取得最大值4a，
则a(a+1)2+a(a+1)-2a=4a，
解得a=-4或1，
综上所述所求a的值为-3或2或-4或1．
