题目内容
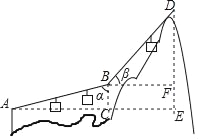
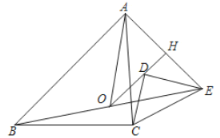
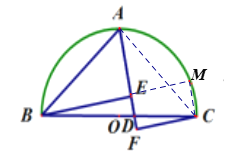
【题目】如图,点A是以BC为直径的半圆的中点,连接AB,点D是直径BC上一点,连接AD,分别过点B、点C向AD作垂线,垂足为E和F,其中,EF=2,CF=6,BE=8,则AB的长是( )
A.4B.6C.8D.10
【答案】D
【解析】
延长BE交![]() 于点M,连接CM,AC,依据直径所对的圆周角是90度,及等弧对等弦,得到直角三角形BMC和等腰直角三角形BAC,依据等腰直角三角形三边关系,知道要求AB只要求直径BC,直径BC可以在直角三角形BMC中运用勾股定理求,只需要求出BM和CM,依据三个内角是直角的四边形是矩形,可以得到四边形EFCM是矩形,从而得到CM和EM的长度,再用BE+EM即得BM,此题得解.
于点M,连接CM,AC,依据直径所对的圆周角是90度,及等弧对等弦,得到直角三角形BMC和等腰直角三角形BAC,依据等腰直角三角形三边关系,知道要求AB只要求直径BC,直径BC可以在直角三角形BMC中运用勾股定理求,只需要求出BM和CM,依据三个内角是直角的四边形是矩形,可以得到四边形EFCM是矩形,从而得到CM和EM的长度,再用BE+EM即得BM,此题得解.
解:延长BE交![]() 于点M,连接CM,AC,
于点M,连接CM,AC,
∵BC为直径,
∴![]() ,
,![]()
又∵由![]() 得:
得:![]() ,
,
∴四边形EFCM是矩形,
∴MC=EF =2,EM=CF=6
又∵BE=8,
∴BM=BE+EM=8+6=14,
∴![]() ,
,
∵点A是以BC为直径的半圆的中点,
∴AB=AC,
又∵![]() ,
,
∴![]() ,
,
∴AB=10.
故选:D.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
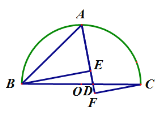
综合自测系列答案【题目】如图,半圆O的直径AB=5cm,点M在AB上且AM=1cm,点P是半圆O上的动点,过点B作BQ⊥PM交PM(或PM的延长线)于点Q.设PM=xcm,BQ=ycm.(当点P与点A或点B重合时,y的值为0)小石根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.下面是小石的探究过程,请补充完整:
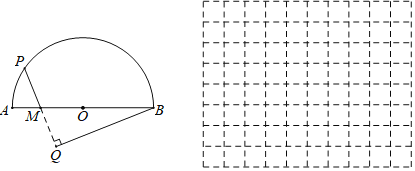
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm | 0 | 3.7 | ______ | 3.8 | 3.3 | 2.5 | ______ |
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当BQ与直径AB所夹的锐角为60°时,PM的长度约为______cm.