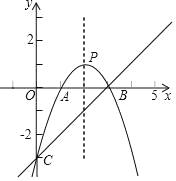Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°ŅĺŇńÍľ∂ ż—ß–ň»§–°◊ťĺ≠Ļż –≥°Ķų≤ť£¨Ķ√ĶĹń≥÷÷‘ň∂Į∑Ģ√Ņ‘¬ĶńŌķŃŅ « ŘľŘĶń“ĽīőļĮ ż£¨«“ŌŗĻō–ŇŌĘ»ÁŌ¬ĪŪ£ļ
ŘľŘ£®‘™/ľĢ£© | 100 | 110 | 120 | 130 | °≠ |
‘¬ŌķŃŅ£®ľĢ£© | 200 | 180 | 160 | 140 | °≠ |
“—÷™ł√‘ň∂Į∑ĢĶńĹÝľŘő™√ŅľĢ60‘™£¨…Ť ŘľŘő™x‘™£ģ
£®1£©«Ž”√ļ¨xĶń Ĺ◊”ĪŪ ĺ£ļĘŔŌķ Řł√‘ň∂Į∑Ģ√ŅľĢĶńņŻ»ů «£®°° °°£©‘™£Ľ
£®2£©«ů‘¬ŌķŃŅy”Ž ŘľŘxĶń“ĽīőļĮ żĻōŌĶ Ĺ£ļ
£®3£©…ŤŌķ Řł√‘ň∂Į∑ĢĶń‘¬ņŻ»ůő™W‘™£¨ń«√ī ŘľŘő™∂ŗ…Ŕ‘™ Ī£¨ĶĪ‘¬ĶńņŻ»ů◊Óīů£Ņ◊ÓīůņŻ»ů «∂ŗ…Ŕ‘™£Ņ
°ĺīūįł°Ņ£®1£©ĘŔx©Ā60‘™£Ľ£®2£©y£Ĺ©Ā2x+400£Ľ£®3£© ŘľŘő™130‘™ Ī£¨ĶĪ‘¬ĶńņŻ»ů◊Óīů£¨◊ÓīůņŻ»ů «9800‘™
°ĺĹ‚őŲ°Ņ
£®1£©łýĺ›ņŻ»ů£Ĺ ؾةĀĹݾثů≥ŲņŻ»ů£Ľ
£®2£©‘ň”√īż∂®ŌĶ ż∑®«ů≥Ų‘¬ŌķŃŅy”Ž ŘľŘxĶń“ĽīőļĮ żĻōŌĶ ĹľīŅ…£Ľ
£®3£©łý囑¬ņŻ»ů£Ĺ√ŅľĢĶńņŻ»ů°Ń‘¬ŌķŃŅŃ–≥ŲļĮ żĻōŌĶ Ĺ£¨łýĺ›∂ĢīőļĮ żĶń–‘÷ «ů≥Ų◊ÓīůņŻ»ů£ģ
Ĺ‚£ļ£®1£©Ōķ Řł√‘ň∂Į∑Ģ√ŅľĢĶńņŻ»ů «£ļ£®x©Ā60£©‘™£¨
Ļ īūįłő™£ļx©Ā60£Ľ
£®2£©…Ť‘¬ŌķŃŅy”ŽxĶńĻōŌĶ Ĺő™y£Ĺkx+b£¨
”…Ő‚“‚Ķ√£¨![]() £¨
£¨
Ĺ‚Ķ√![]() £ģ
£ģ
‘Úy£Ĺ©Ā2x+400£Ľ
£®3£©”…Ő‚“‚Ķ√£¨W£Ĺ£®x©Ā60£©£®©Ā2x+400£©
£Ĺ©Ā2x2+520x©Ā24000
°ŗĶĪx£Ĺ130 Ī£¨ņŻ»ů◊Óīů÷Ķő™9800‘™£¨
Ļ ŘľŘő™130‘™ Ī£¨ĶĪ‘¬ĶńņŻ»ů◊Óīů£¨◊ÓīůņŻ»ů «9800‘™£ģ

°ĺŐ‚ńŅ°Ņń≥–£ĺŇńÍľ∂ŃĹłŲįŗ£¨łų—°Ň…10√Ż—ß…ķ≤őľ”—ß–£ĺŔ––Ķń°įļļ◊÷Őż–ī°Īīů»Ł‘§»Ł£ģłų≤ő»Ł—° ÷Ķń≥…ľ®»ÁÕľ£ļ
ĺŇ£®1£©įŗ£ļ88£¨91£¨92£¨93£¨93£¨93£¨94£¨98£¨98£¨100
ĺŇ£®2£©įŗ£ļ89£¨93£¨93£¨93£¨95£¨96£¨96£¨98£¨98£¨99
Õ®Ļż’ŻņŪ£¨Ķ√ĶĹ żĺ›∑÷őŲĪŪ»ÁŌ¬£ļ
įŗľ∂ | ◊ÓłŖ∑÷ | ∆Ĺĺý∑÷ | ÷–őĽ ż | ÷ŕ ż | ∑Ĺ≤Ó |
ĺŇ£®1£©įŗ | 100 | m | 93 | 93 | 12 |
ĺŇ£®2£©įŗ | 99 | 95 | n | 93 | 8£ģ4 |
£®1£©÷ĪĹ”–ī≥ŲĪŪ÷–m°ĘnĶń÷Ķ£Ľ
£®2£©“ņĺ› żĺ›∑÷őŲĪŪ£¨”–»ňňĶ£ļ°į◊ÓłŖ∑÷‘ŕ£®1£©įŗ£¨£®1£©įŗĶń≥…ľ®Ī»£®2£©įŗļ√°Ī£¨Ķę“≤”–»ňňĶ£®2£©įŗĶń≥…ľ®“™ļ√£¨«ŽłÝ≥ŲŃĹŐű÷ß≥÷ĺŇ£®2£©įŗ≥…ľ®ļ√ĶńņŪ”…£Ľ
£®3£©»Űī”ŃĹįŗĶń≤ő»Ł—° ÷÷–—°ňń√ŻÕ¨—ß≤őľ”ĺŲ»Ł£¨∆š÷–ŃĹłŲįŗĶńĶŕ“Ľ√Ż÷ĪĹ”ĹÝ»ŽĺŲ»Ł£¨ŃŪÕ‚ŃĹłŲ√Ż∂Ó‘ŕňńłŲ°į98∑÷°ĪĶń—ß…ķ÷–»ő—°∂ĢłŲ£¨ ‘«ůŃŪÕ‚ŃĹłŲĺŲ»Ł√Ż∂Ó¬š‘ŕÕ¨“ĽłŲįŗĶńłŇ¬ £ģ