题目内容
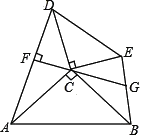
【题目】如图,点 C 为 Rt△ACB 与 Rt△DCE 的公共点,∠ACB=∠DCE=90°,连 接 AD、BE,过点 C 作 CF⊥AD 于点 F,延长 FC 交 BE 于点 G.若 AC=BC=25,CE=15, DC=20,则![]() 的值为___________.
的值为___________.
【答案】![]()
【解析】
过 E作 EH⊥GF于 H,过 B作 BP⊥GF于 P,依据△EHG∽△BPG,可得![]() =
=![]() ,再根据△DCF∽△CEH,△ACF∽△CBP,即可得到 EH=
,再根据△DCF∽△CEH,△ACF∽△CBP,即可得到 EH=![]() CF,BP=CF,进 而得出
CF,BP=CF,进 而得出![]() =
=![]() .
.
如图,过 E作 EH⊥GF于 H,过 B 作 BP⊥GF于P,则∠EHG=∠BPG=90°,
又∵∠EGH=∠BGP,
∴△EHG∽△BPG,
∴![]() =
=![]() ,
,
∵CF⊥AD,
∴∠DFC=∠AFC=90°,
∴∠DFC=∠CHF,∠AFC=∠CPB, 又∵∠ACB=∠DCE=90°,
∴∠CDF=∠ECH,∠FAC=∠PCB,
∴△DCF∽△CEH,△ACF∽△CBP,
∴![]() ,
,
∴EH=![]() CF,BP=CF,
CF,BP=CF,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目