题目内容
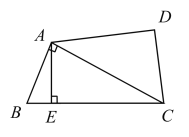
【题目】如图,在△ABC中, AD是∠BAC的平分线,DF⊥AB,DM⊥AC,垂足分别为F、M,AF=10cm ,BF=6cm ,AC=14cm.动点E以3cm/s的速度从A点向B点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t s.当t=__________s时, △DFE与△DMG全等.(写出符合题意的t的所有取值)

【答案】3或![]()
【解析】
先根据AB、AC的长、及点E、G的运动速度求出t的取值范围,再根据角平分线的性质、直角三角形全等的判定定理与性质求出CM的长,然后根据![]() 与
与![]() 全等,得出
全等,得出![]() ,据此建立方程求解即可.
,据此建立方程求解即可.
![]()
![]()
则点E从点A运动到点B时,运动时间![]() ;点G从点C运动到点A时,运动时间
;点G从点C运动到点A时,运动时间![]()
由题意可得,运动时间t的取值范围为![]()
![]() 是
是![]() 的平分线,
的平分线,![]()
![]()
![]()
![]()
则点E从点A运动到点F时,运动时间![]() ,此时,点G从点C开始运动的距离为
,此时,点G从点C开始运动的距离为![]() ,即当点E在AF上时,点G一定在CM上
,即当点E在AF上时,点G一定在CM上
若![]() 与
与![]() 全等,则
全等,则![]() ,由题意,分以下3种情况:
,由题意,分以下3种情况:
(1)当点E在AF上时,![]()
则![]() ,解得
,解得![]() ,符合要求
,符合要求
(2)当点E在BF上,点G在CM上时,![]()
则![]() ,解得
,解得![]() ,符合要求
,符合要求
(3)当点E在BF上,点G在AM上时,![]()
则![]() ,解得
,解得![]() ,此时
,此时![]() ,不符题意,舍去
,不符题意,舍去
综上,t的值为3或![]()
故答案为:3或![]() .
.

【题目】甲、乙两名同学分别进行6次射击训练,训练成绩(单位:环)如下表
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六交 | |
甲 | 9 | 8 | 6 | 7 | 8 | 10 |
乙 | 8 | 7 | 9 | 7 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是( )
A. 他们训练成绩的平均数相同 B. 他们训练成绩的中位数不同
C. 他们训练成绩的众数不同 D. 他们训练成绩的方差不同
【题目】为了从甲、乙两名选手中选拔出一个人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表.
甲、乙射击成绩统计表
平均数(环) | 中位数(环) | 方差 | 命中10环的次数 |
甲 | 7 | 0 | |
乙 | 1 |
甲、乙射击成绩折线统计图

(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?