Question

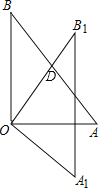
【题目】如图，在平面直角坐标系中，为坐标原点．一次函数的图象与x轴交于点，与y轴交于点B，与正比例函数的图象交于点．

（1）求一次函数的解析式；

（2）在x轴上寻找点P，使得为等腰三角形，直接写出所有满足条件的点P的坐标；

（3）在直线AB上寻找点Q，使得，求点Q的坐标．

Answer 1

【答案】（1）一次函数的解析式为；（2）点P的坐标为或或或；（3）点Q的坐标为或．

【解析】

（1）可先求得C点坐标，再利用待定系数法可求得一次函数的表达式；
（2）可设P（x，0），则可表示出CP、OP和OC，分CP=OP、CP=OC和OP=OC三种情况，分别得到关于x的方程，可求得P点的坐标；
（3）可设出Q点的坐标，从而可表示出CQ的长，由三角形的面积可得到关于Q点坐标的方程，可求得Q点的坐标．

(1)∵正比例函数的图象过点，

∴，

∴点C的坐标为．

设直线AB的解析式为，

把A，C两点的坐标代入可得，解得，

∴一次函数的解析式为．

(2)设P点坐标为，C点坐标为，

∴，，．

∵为等腰三角形，

∴有，和三种情况：

①当时，即，

解得：，此时点P的坐标为；

②当时，即，

解得：(舍去)或，此时点P的坐标为；

③当时，即，解得或，

此时点P的坐标为或．

综上所述，点P的坐标为或或或．

(3)∵点Q在直线AB上，

∴设点Q的坐标为．

∵点C的坐标为，

∴．

∵在中，令可得，

∴点B的坐标为，∴，

∴，且．

如图，过点O作于点D，

∴，即，

解得：，

．

,

∴，解得或．

当时， ，

当时，．

故点Q的坐标为或．