题目内容
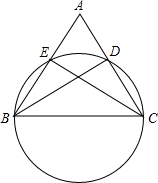
如图，已知∠OCB=20°，则∠A= ▲ 度．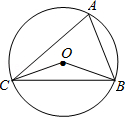
70°。
由OB=OC与∠OCB=20°，根据等边对等角的性质，即可求得∠OBC=20°。
由三角形内角和定理，得∠BOC=180°﹣∠OCB﹣∠OBC=180°﹣20°﹣20°=140°。
由同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半的性质，即可求得∠A=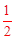
∠BOC=70°。
由三角形内角和定理，得∠BOC=180°﹣∠OCB﹣∠OBC=180°﹣20°﹣20°=140°。
由同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半的性质，即可求得∠A=
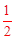∠BOC=70°。
练习册系列答案
名校课堂系列答案
相关题目
绕点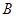
逆时针旋转到
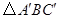使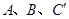
在同一直线上，若
，
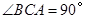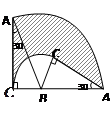
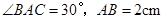，则图中阴影部分面积为 cm2。
