Question

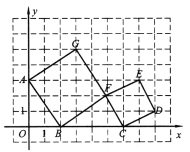
【题目】如图，在平面直角坐标系中，，，且满足方程组，连接，．

（1）求的面积；

（2）动点从点出发，以每秒个单位长度的速度沿轴向左运动，连接，设点运动的时间为秒， 的面积为， 试用含的式子表示；

（3）在的条件下，点，点是上一点，连接，点在延长线上，且，连接， 当点在轴负半轴上，，， 四边形的面积与的面积比为时，求此时值和点的坐标．

Answer 1

【答案】（1）6；（2）；（3）此时t的值为，点E的坐标为（3，）．

【解析】

（1）利用加减消元法解方程组即可求解；

（2）分类讨论：当点P在点O右侧时，当点P在点O左侧时，利用三角形的面积公式表示即可；

（3）根据题意画出相应的示意图，在x轴上取点F，使得MF＝MB，连接FE、FN，在x轴的正半轴上取一点P '，使得OP'＝OP，连接AP'，过点N作NH⊥AB于点H，先证△P'AB≌△EFB，可得BE＝8－2t，再证△NHB≌△AOP可得NH＝AO＝3，进而可表示出四边形的面积与的面积，最后根据面积之比为49：10列出方程求解即可求得t的值，再过点E作EG⊥x轴于点G，进而可证得△EGB∽△AOB，通过相似三角形的性质即可求得点E的坐标．

解：（1）

①×3＋②×2，得

13a＝39，

a＝3，

将a＝3代入②得

b＝4，

∴原方程组的解为

∴A（0，3），B（4，0），

∴OA=3，OB＝4，

∴

答：的面积为6；

（2）当0＜t≤2时，

，

当t＞2时，

，

综上所述：

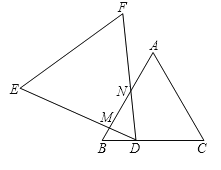
（3）如图，在x轴上取点F，使得MF＝MB，连接FE、FN，在x轴的正半轴上取一点P '，使得OP'＝OP，连接AP'，过点N作NH⊥AB于点H，

∵MF＝MB，ME＝MN，

∴四边形EFNB为平行四边形，

∴EF∥BN，

∴∠EFB＝∠FBN，

∵OP'＝OP，OA⊥x轴，

∴AP'＝AP，

∴∠APO＝∠AP'O，

∵∠APO＝∠ABN，

∴∠AP'O＝∠ABN，

∴∠P'AB＋∠ABP'＝∠FBN＋∠ABP'，

∴∠P'AB＝∠FBN，

∴∠EFB＝∠P'AB，

∵点M（1.5，0），点B（4，0）

∴MF＝MB＝2.5，

∴BF＝5，

∵AB＝5，

∴AB＝BF，

在△P'AB与△EFB中，

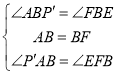
∴△P'AB≌△EFB（ASA）

∴BE＝BP'，

∵BP＝2t，BO＝4,

∴OP'＝OP＝2t－4，

∴BE＝BP'＝OB－OP'＝4－(2t－4)＝8－2t，

∵NH⊥AB，∠AOP＝90°，

∴∠NHB＝∠AOP＝90°，

在△NHB与△AOP中，

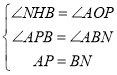
∴△NHB≌△AOP（AAS）

∴NH＝AO＝3，

∴

∵ME＝MN，

∴

，

∵

∴

∵

∴ ，

解得

则BE＝8－2t＝

如图，过点E作EG⊥x轴于点G，

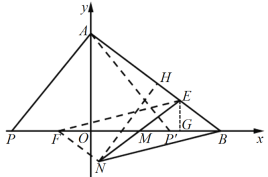
则EG∥y轴，

∴△EGB∽△AOB，

∴

∴

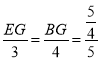
解得，，

∴

∴点E的坐标为（3，）

答：此时t的值为，点E的坐标为（3，）．