题目内容
【题目】抛物线y=x2﹣2mx﹣3m2(m>0)与x轴交于A、B两点,A点在B点左边,与y轴交于C点,顶点为M.
(1)当m=1时,求点A、B、M坐标;
(2)如图(1)的条件下,若P为抛物线上一个动点,以AP为斜边的等腰直角的直角顶点Q在对称轴上,(A、P、Q按顺时针方向排列),求P点坐标.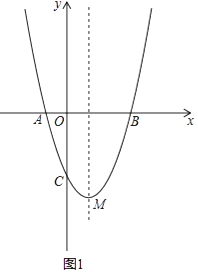
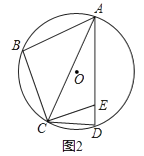
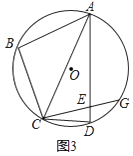
(3)如图2,若一次函数y=kx+b过B点且与抛物线只有一个公共点,平移直线y=kx+b,使其过抛物线的顶点M,与抛物线另一个交点为D,与x轴交于F点,当m变化时,求证:DF:MF是定值.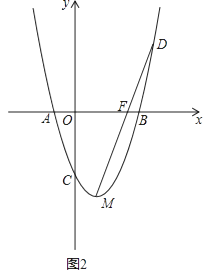
【答案】
(1)解:当m=1时,抛物线解析式为y=x2﹣2x﹣3,
当y=0时,x2﹣2x﹣3=0,解得x1=﹣1,x2=3,则A(﹣1,0),B(3,0);
∵y=(x﹣1)2﹣4,
∴M点坐标为(1,﹣4);
(2)解:抛物线的对称轴为直线x=1,直线x=1交x轴于N,设P(t,t2﹣2t﹣3),Q(1,a)
作PH⊥直线x=1于点H,如图,
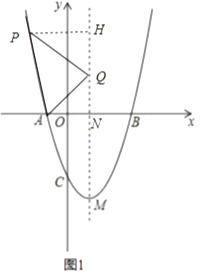
∵△APQ为等腰直角三角形,
∴PQ=AQ,∠AQP=90°,
∵∠AQH+∠AQN=90°,∠AQN+∠QAN=90°,
∴∠PQH=∠QAN,
在△PQH和△QAN中
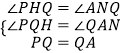 ,
,
∴△PQH≌△QAN,
∴QH=AN,PH=QN,
即t2﹣2t﹣3﹣a=2,1﹣t=a,
∴t2﹣2t﹣3﹣(1﹣t)=2,
整理得t2﹣t﹣5=0,解得t1= ![]() ,t2=
,t2= ![]() ,
,
∴P点坐标为( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() );
);
(3)解:证明:y=x2﹣2mx﹣3m2=(x﹣m)2﹣4m2,则M(m,﹣4m2),
当y=0时,x2﹣2mx﹣3m2=0,解得x1=﹣m,x2=3m,则B(3m,0),
把B(3m,0)代入y=kx+b得3mk+b=0,解得b=﹣3mk,
则直线y=kx+b的解析式表示为y=kx﹣3mk,
∵一次函数y=kx﹣3mk与抛物线只有一个公共点,
∴方程x2﹣2mx﹣3m2=kx﹣3mk有相等的实数解,
方程整理为x2﹣(2m+k)x﹣3m2+3mk=0,
∵△=(2m+k)2﹣4(﹣3m2+3mk)=0,
∴k=4m,
∴一次函数y=kx+b表示为y=4mx﹣12m2,
设直线y=kx+b平移后的解析式为y=4mx+n,
把M(m,﹣4m2)代入得﹣4m2=﹣4m2+n,解得n=﹣8m2,
即经过点D的直线解析式为y=4mx﹣8m2,
当y=0时,4mx﹣8m2=0,解得x=2m,则F(2m,0)
解方程组 ![]() 得
得 ![]() 或
或 ![]() ,则D(5m,12m2)
,则D(5m,12m2)
作AG⊥x轴于E,MG∥x轴,它们相交于点G,如图2,

∵EF∥MG,
∴ ![]() =
= ![]() =
= ![]() =3.
=3.
【解析】(1)把m=1代入得到抛物线的解析式,然后利用配方法可求得点M的坐标,接下来,令y=0可求得对应的x的值,从而可得到点A和点B的坐标;
(2)设P(t,t2﹣2t﹣3),Q(1,a),作PH⊥直线x=1于点H,首先证明△PQH≌△QAN,依据全等三角形的性质可得到QH=AN,PH=QN,从而可得到关于a、t的方程组,解方程组可求得点P的坐标;
(3)作AG⊥x轴于E,MG∥x轴,它们相交于点G,利用配方法求得抛物线的顶点坐标为M(m,﹣4m2),然后令y=0可求得B(3m,0),把B(3m,0)代入y=kx+b得3mk+b=0,求得b的值,从而得直线的解析式为y=kx﹣3mk,接下来,将y=kx﹣3mk代入抛物线的解析式,得到关于x的方程,然后由一次函数y=kx﹣3mk与抛物线只有一个公共点可得到△=0,从而可得到k与m的关系,设直线y=kx+b平移后的解析式为y=4mx+n,把点M的坐标代入可得到n=﹣8m2,则经过点D的直线解析式为y=4mx﹣8m2,然后再求得点F的坐标,解方程组可求得点D的坐标,最后,依据平行线分线段成比例定理求解即可.